傅里叶变换

傅里叶变换学习笔记，简单总结了下，主要还是理解了下它的作用。

傅里叶变换§

首先，变换这个过程是可逆的，直观的图像的旋转是变换，傅里叶变换也是变换，因此有使用傅里叶变换对图像、视频进行压缩，因为图像的频谱图上很多像素点都接近于0，可以达到压缩大小的效果。

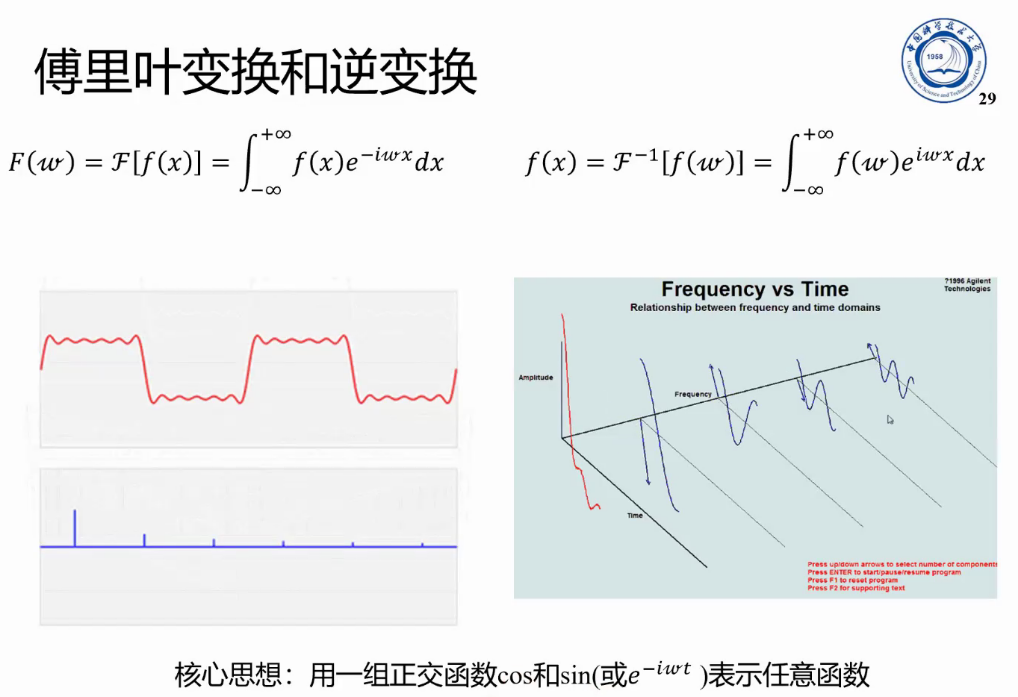
对于定义，简单的理解，傅里叶变换就是将时域中的信号分解为了多个不同频率的正弦和余弦信号，计算不同的正余弦信号与原始信号相交后的积分面积，若积分面积为0，则说明这两个信号完全不相似，是不会由另一个信号组合而来的。积分面积不为0，它的大小就为对应频率的正余弦波的幅度。

为什么会既使用正弦，又使用余弦？其实拆分的信号应该说是正余弦信号的组合，正弦与余弦相加用来构成不同的相位。

在已经幅度、相位和频率后，就可以转换为对应的正余弦信号，一组正余弦信号又可以还原为原始信号。

对于为什么可以使用$e^{-iwx}$，是因为可以使用欧拉公式拆分为$sinx$和$cosx$的形式。 $$ e^{ix} = \cos{x} + i\sin{x} $$

离散傅里叶变换（DFT）§

在实际应用中，因为通过采样得到的时域上的信号是离散的点，并没有办法像连续函数那样进行积分，因此需要使用到离散傅里叶变换。

快速傅里叶变换（FFT）§

由于离散傅里叶变换的时间复杂度为$O(N^2)$，对于$N$个时域上的离散点，要与$N$个正余弦信号进行运算。

在快速傅里叶变换中，考虑到部分的信号会与部分的离散点的运算结果相同，因此可以只计算一次，从而减小运算量。对于$N$个离散点，是可以拆分为$\log_{2}{N}$个只包含两个离散点的时域图，然后再与$N$个信号进行运算，此时快速傅里叶变换的复杂度为$O(N\log_{2}{N})$。

尝试使用了快速傅里叶变换，从时域转换到了频域上，发现效果是极差，根本就训练不起来，很疑惑。所以查了下资料，有说快速傅里叶变换得到的频域图并不能捕获到局部性的特征，因为对于不同的时域图，可能在这个时间范围内是有相同的频域图的，因为频域上是这一段时间上的统计值，所以为了解决这个问题，下面就有提到短时傅里叶变换和小波变换。

参考链接：https://blog.csdn.net/u011442170/article/details/105934323

短时傅里叶变换§

• 解决了快速傅里叶变换的局部性问题

• 使用一个固定的窗口，仅对窗口内的信号进行快速傅里叶变换，这样就可以得到与时间相关的频域变换，进行时频分析。

• 设置不同的窗口，对时间与频率的分辨率有影响，窗口大，频率维度分辨率高，窗口小，时间维度分辨率高，因此最好的情况是在频率比较大的信号上使用小窗口，在频率比较小的信号上使用大窗口，但由于短时傅里叶变换使用的是固定窗口，所以并不能够很好地解决这个问题。

小波变换（DWT）§

• 小波变换很好地解决了上面的局部性和固定窗口的问题，但解决的方法并不是使用动态的窗口，而是直接从分解上入手。
• 回顾之前的傅里叶变换，对信号分解是使用一组正余弦波，而小波变换的分解就是使用的一组小波，这个小波并不唯一，不像傅里叶变换仅有$w$这一个频率相关的参数，小波具有尺度$\alpha$和平移量$\tau $两个参数，其中尺度与频率有关，平移量与时间有关，这样就可以动态地构造出时间与频率的关系，进行时频分析。

补充：关于傅里叶变换的频率、幅度的求解详情可以参考：

https://blog.csdn.net/weixin_39591031/article/details/110392352