有在看清华马少平老师的跟我学AI系列,感觉讲的挺好的,简单易懂,只不过偏向于了解了解,所以是浅尝辄止,但也能够学习并涉猎到很多知识点。
一、数字识别§
1. 模式匹配§
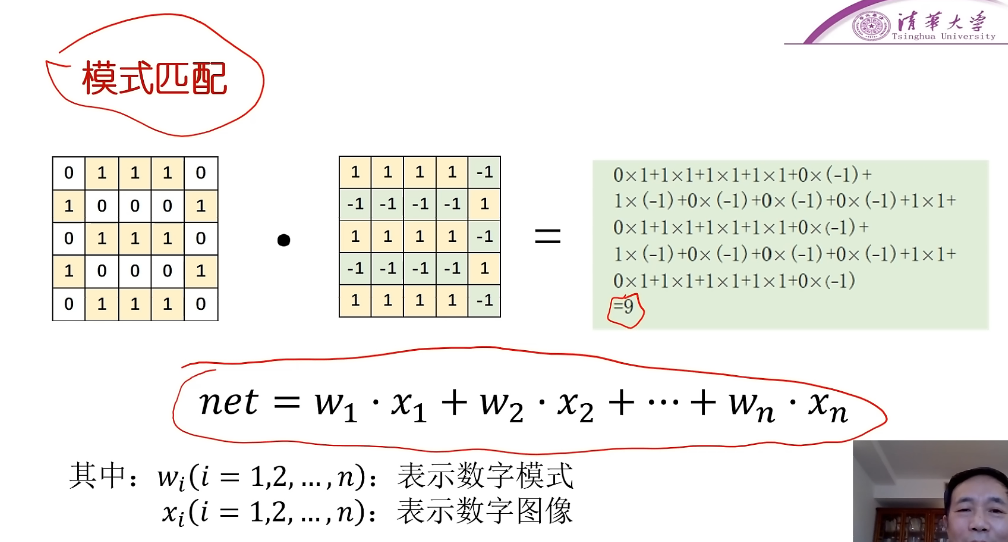
输入*模板,根据匹配值net,值越大,可能性也越大
奖励+惩罚
存在的问题:仅仅根据net值并不一定能准确判断,因为比如1的笔画数很少,那1正确匹配的情况下得到的net值也很小。而对于笔画数多的数字来说,比如模式9,我输入一个1,去匹配模式9,也能够得到一个和直接匹配模式1,差不多的net值,那这就无从判断。也就是说笔画数越多的模式,越有优势,这样的net值比较就会是不合理的。
2. Sigmoid函数§
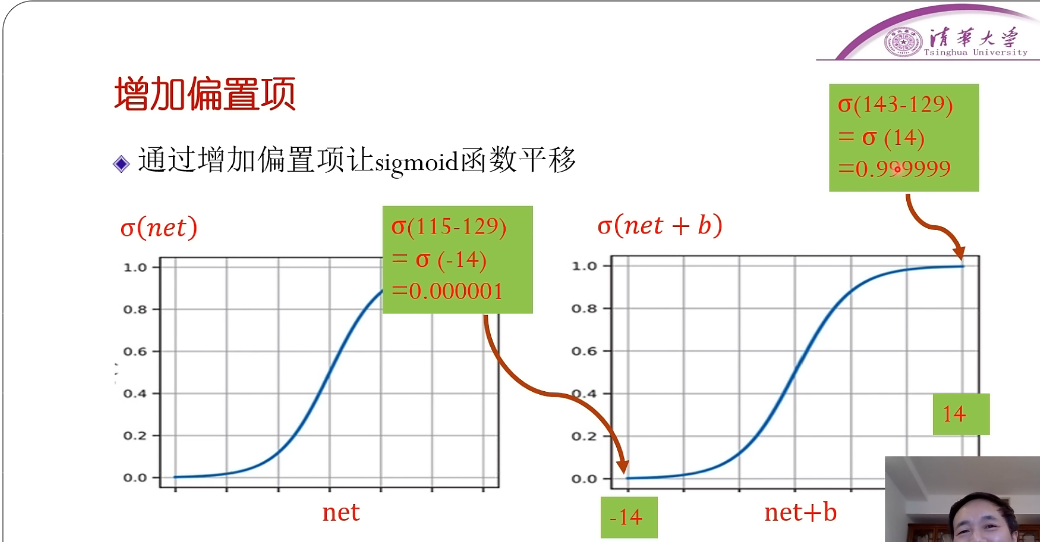
- 选更接近1的
- 但当有两个数都很大的时候,都接近1,就没法判断。此时,就可以增加一个偏执项,可以认为是一个阈值,进行一个偏移。
3. 什么是神经元§
- 神经元,一种模式
4. 神经网络§
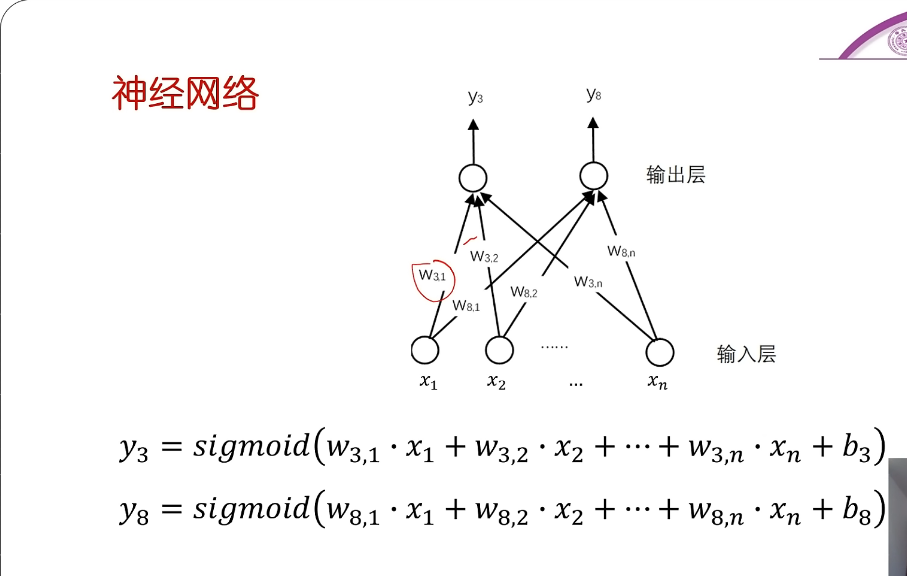
- 由多种神经元所构成的网络
- 不同神经元的权值(包括偏置值)即对应着不同的数字模式
5. 神经网络的横向扩展——增加模式§
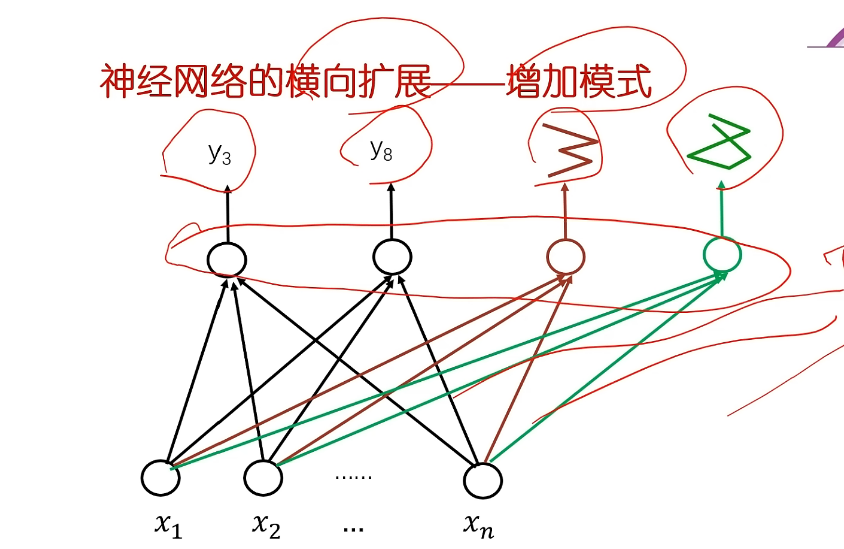
- 增加模式
- 比如有各种长得不一样的3的写法,那就可以去给3增加各种长得不一样的模式,增加神经元。
6. 神经网络的纵向扩展——局部模式§
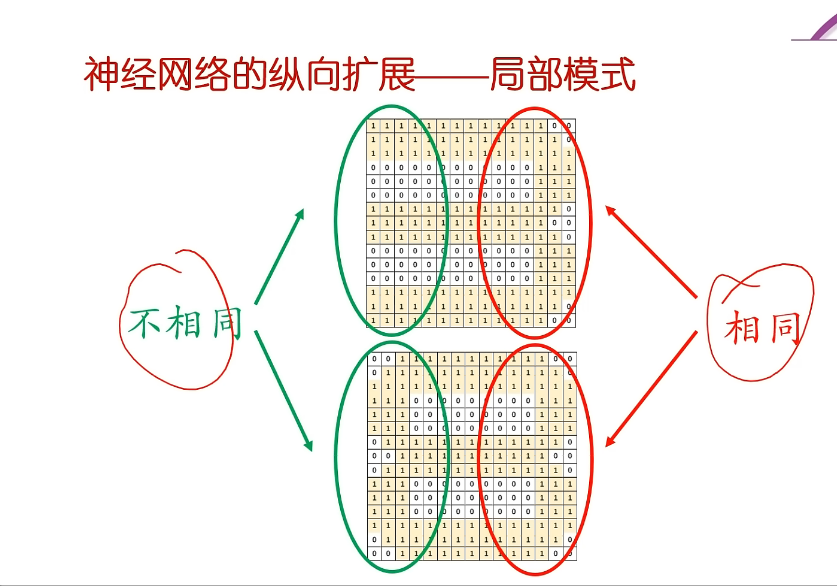
- 将原来的模式进行拆分,这样的话,相同的局部就可以共用了!
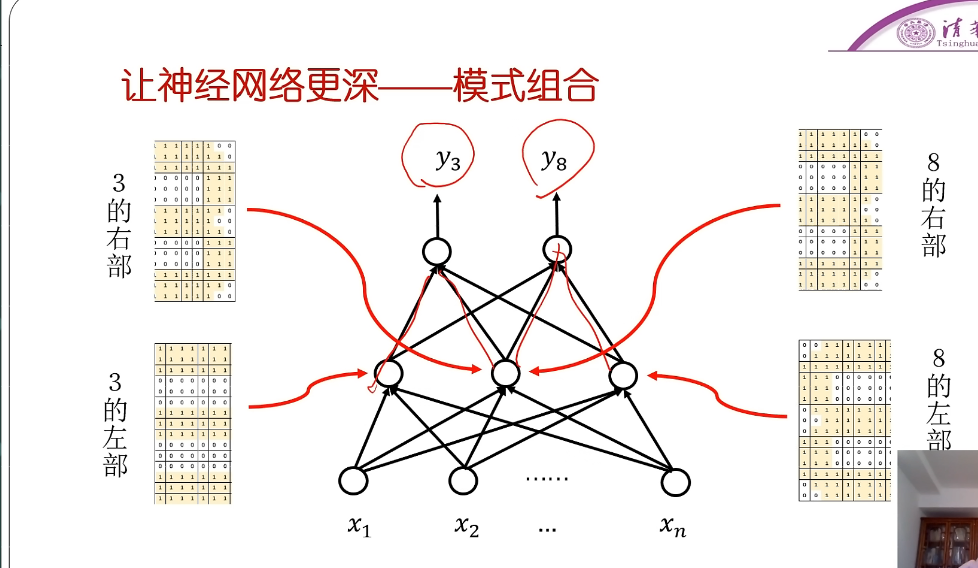
- 越靠近输入的力度越小,越靠近输出力度越大
- 输入为每个像素点,中间为匹配的局部范围内的像素点,不断往后,就可以组成一个全局的模式!
- 根据匹配的程度,匹配的好的神经元,就激活它,让他更有说话的份量。
7. 多层神经网络§
- 每一层计算都是一样的
- 一层一层加深
- 越靠近输入层的神经元,刻画的模式越细致,体现的越是细微信息的特征;越是靠近输出层的神经元,刻画的模式越是体现了整体信息的特征。这样通过不同层次的神经元体现的是不同粒度的特征
8. 如何获得模式§
- 模式通过神经元的连接权重表示(w1、w2、w3、、、b)
- 通过训练样本,自动学习权重,也就是模式(如BP算法)
- 学习到的模式是一种隐含表达。
9. 总结§
- 模式匹配:每一个神经元对应的权值表示一种模式,模式匹配的过程就是输入与当前神经元的权值的加权和,再通过sigmoid函数转换为匹配上的概率,越大说明匹配的越好,则越有可能是正确的。
- 横向与纵向扩展:横向的扩展是增加同一层相同粒度的模式种类的扩展,纵向的扩展是增加不同层不同粒度特征或说是不同粒度局部模式的扩展。
二、神经元与全连接网络§
1. 神经元§
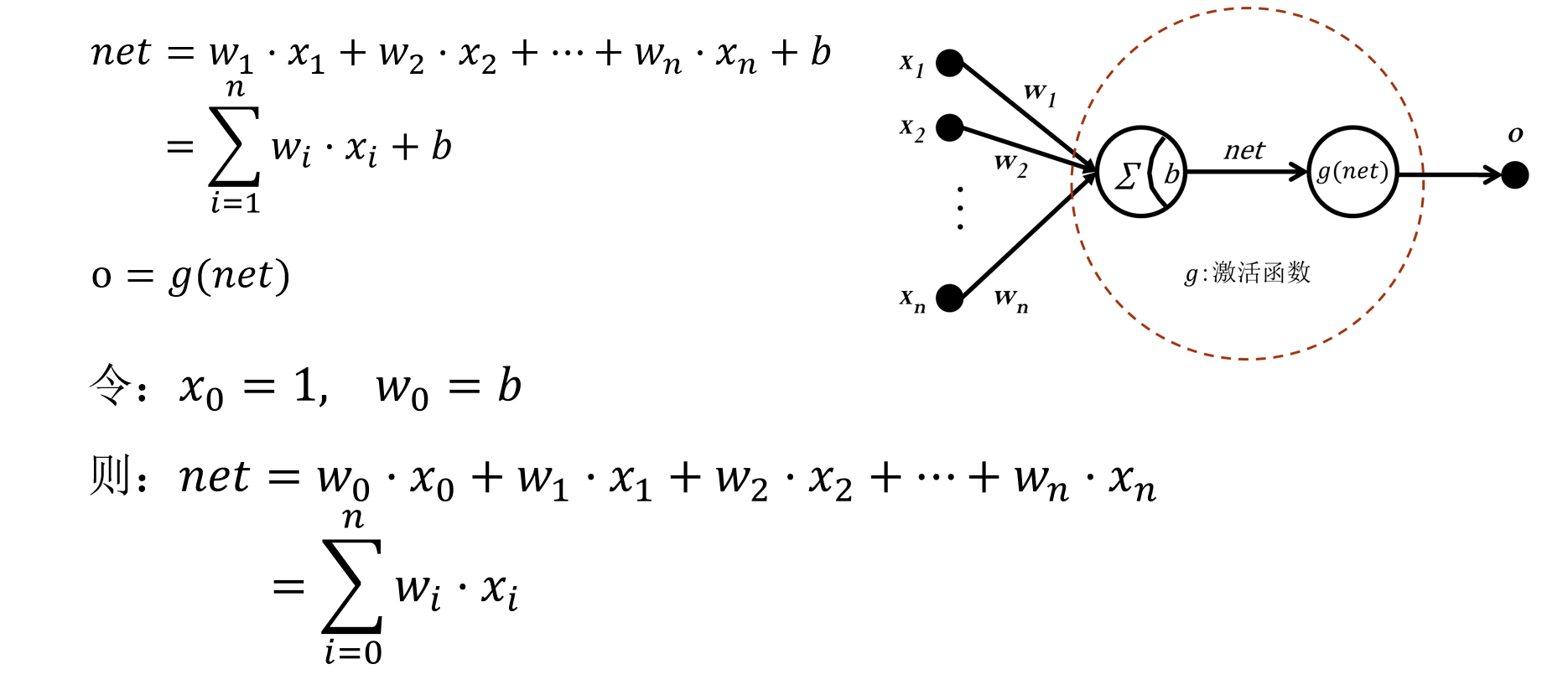
- 根据输入,通过与权重的加权和后,再经过激活函数,得到输出
2. 激活函数§
符号函数(sign函数)§
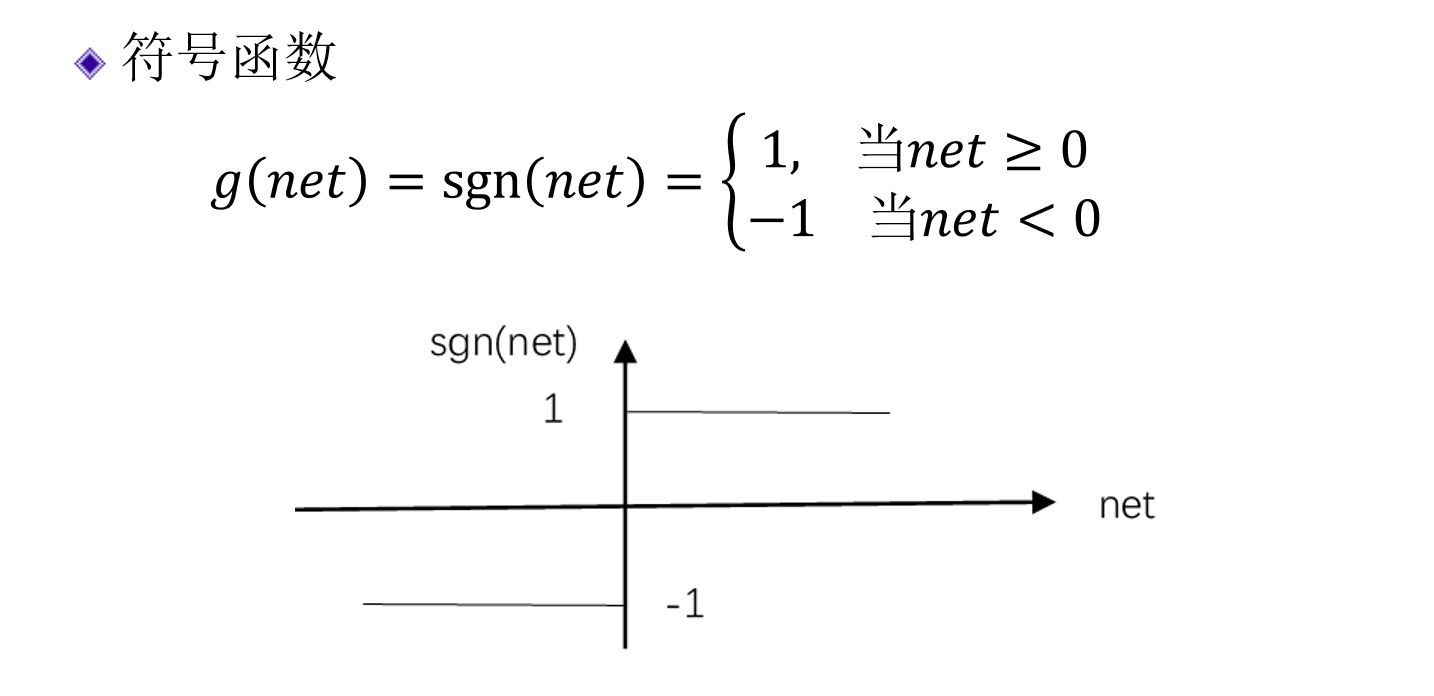
- 最早的激活函数,像单层感知机中就会用到
Sigmoid函数§
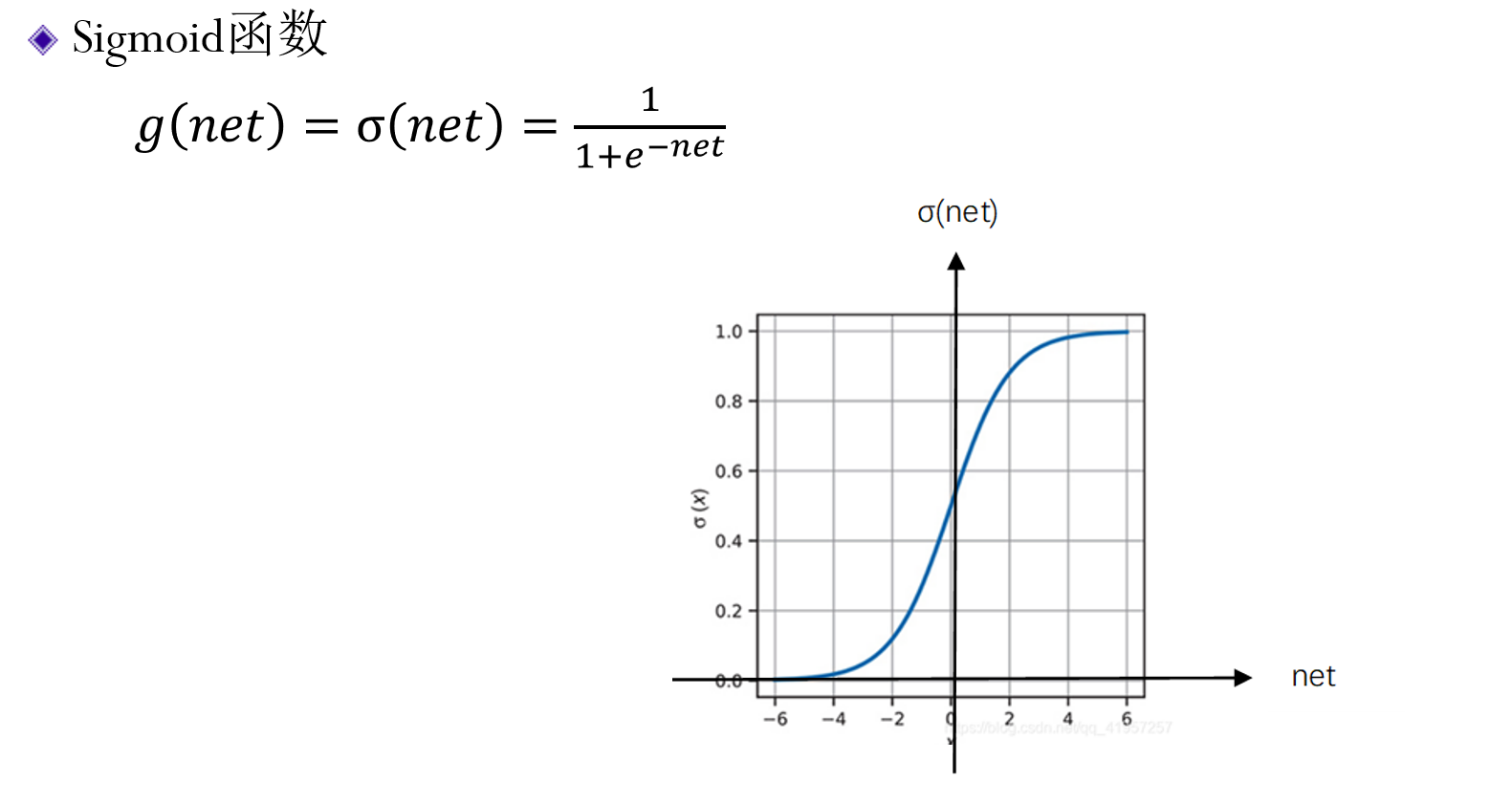
- 输出0~1的范围
- 连续的,可作为概率
双曲正切函数(tanh函数)§
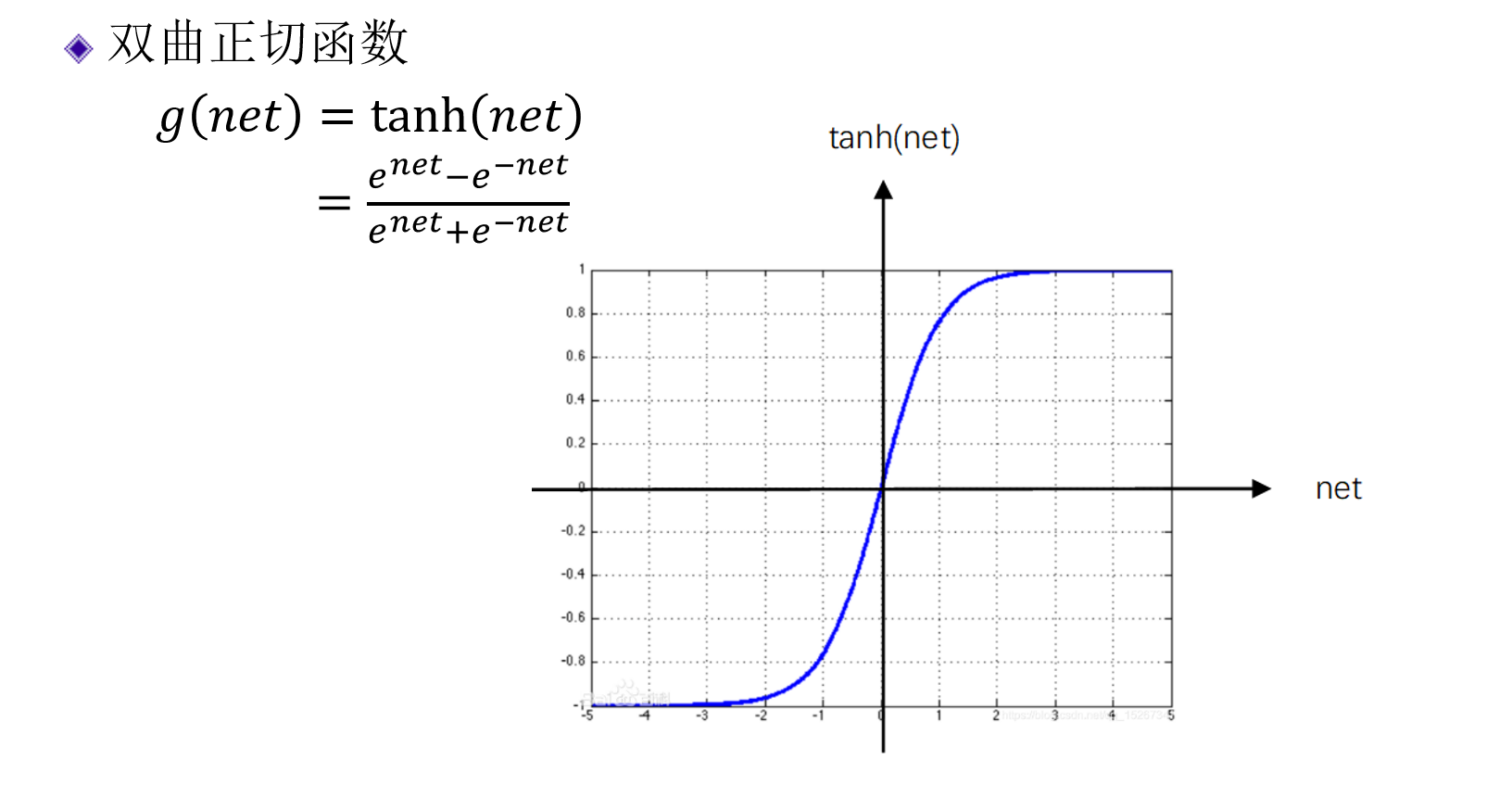
- 和sigmoid函数很像,但是范围不同,范围为-1~1
线性整流函数(ReLu函数)§
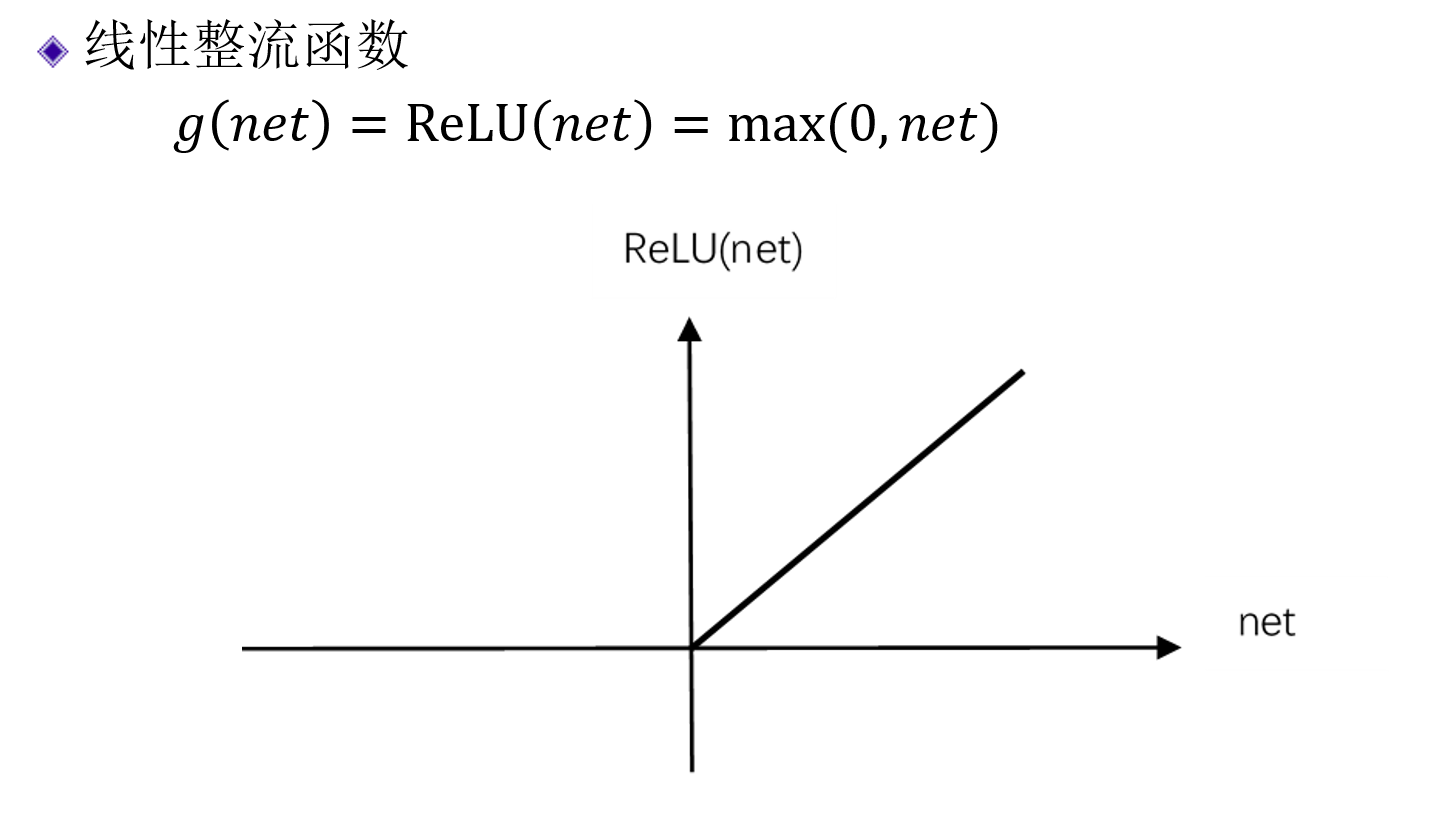
- 整流,像二极管一样,单向通过,即整流
- 经常用于图像处理的问题中
Softmax函数§
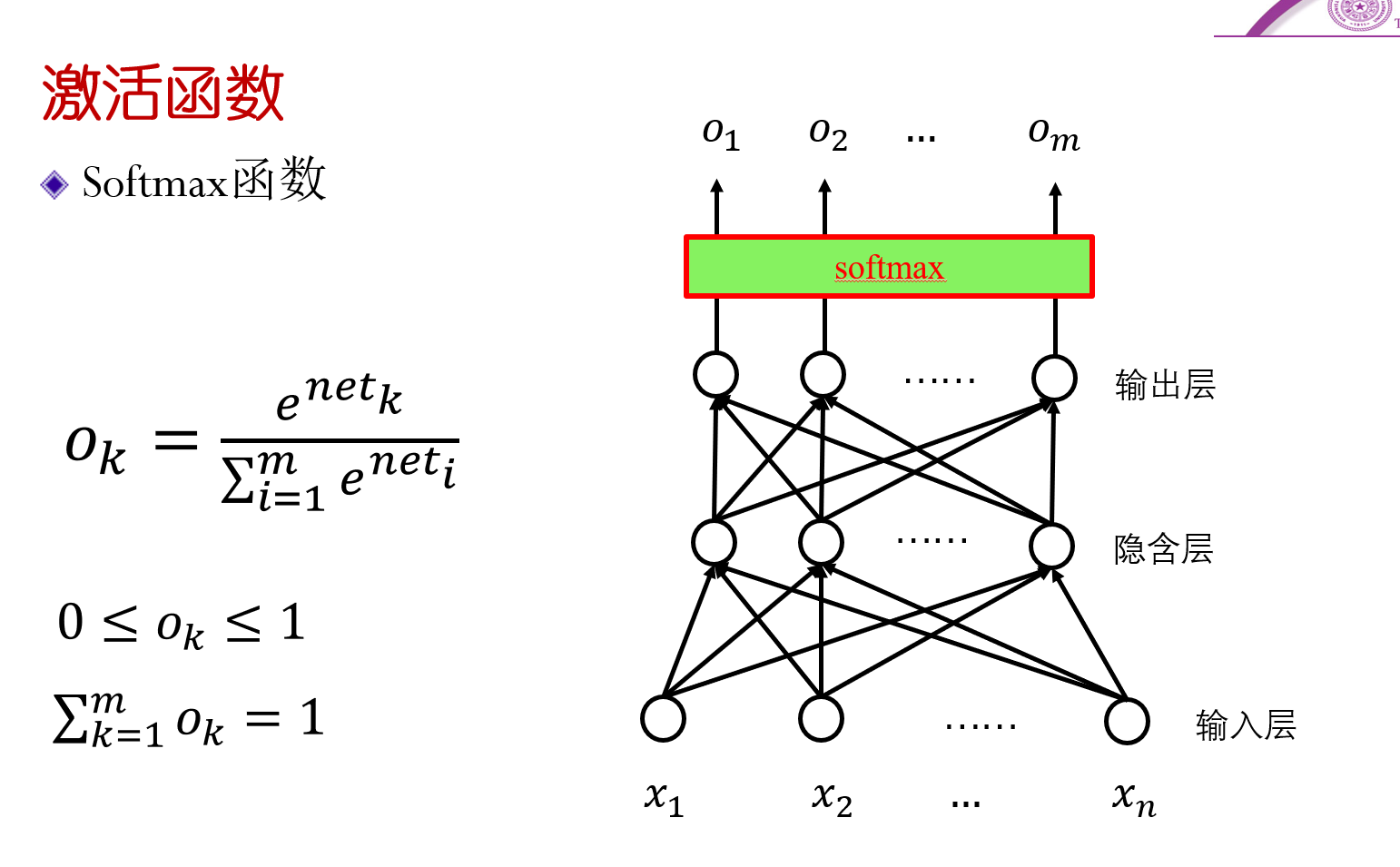
- 一般只用于最后的输出层
- 对输出层的各个神经元的输出的net(加权和)一起通过一个softmax函数,得到各个不同的概率。
3. 全连接网络§
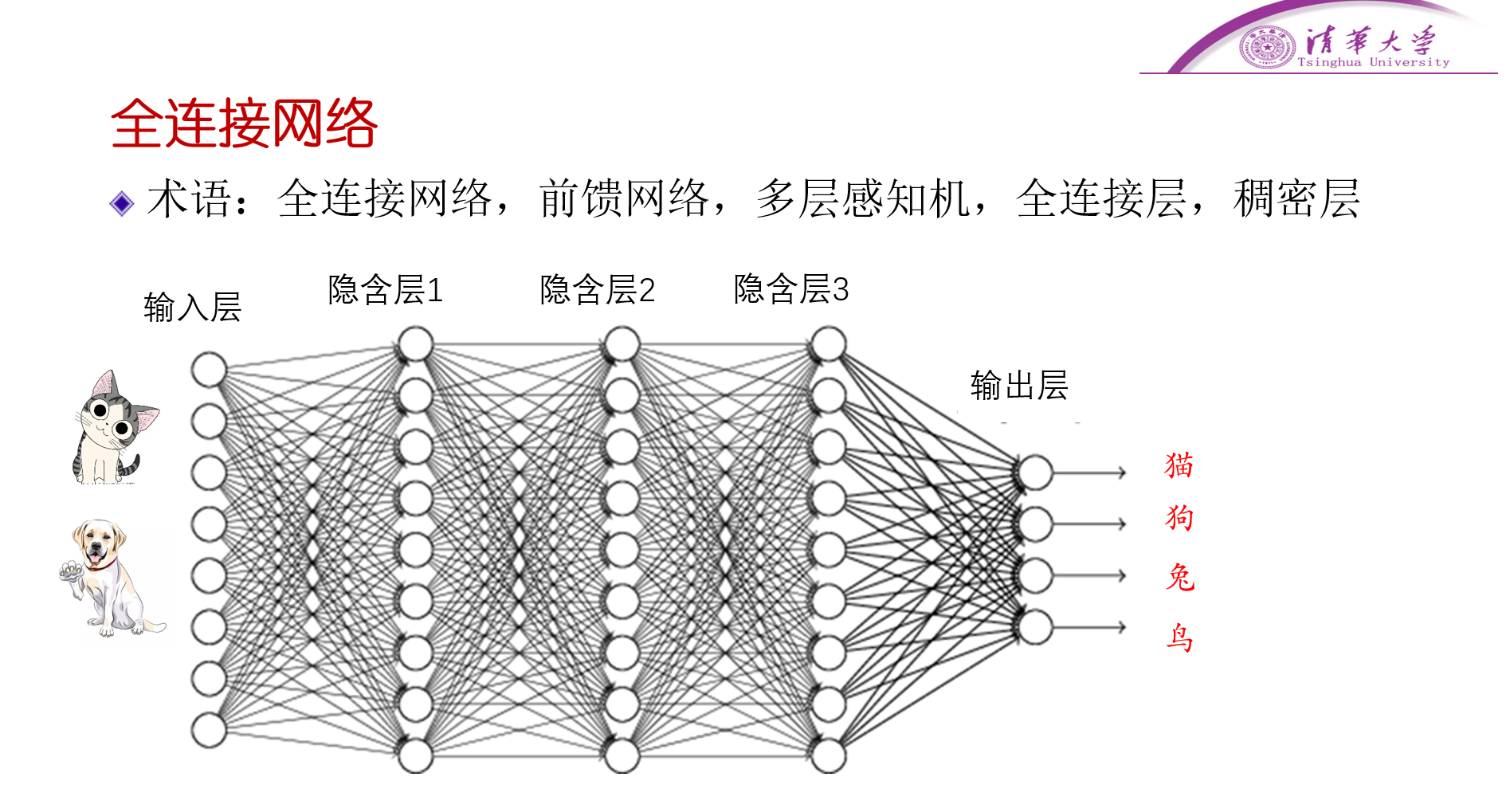
按神经元的连接方式,两层的神经元,两两之间都有连接,每个连接都有权重。
按信息走的方向来说,一层一层往前走,前一层的输出,作为下一层的输入,即前馈网络。
多层感知机MLP,就是全连接网络,一开始都是说感知机的。
全连接层,或稠密层,都是指全连接。
三、神经网络的训练§
收集数据集
数据标注
训练集(平常作业)与测试集(期中期末考试)
- 样本
损失函数-评价调节效果
- 误差平方和
- 为什么用平方
- 为什么前面乘1/2
- 误差平方和
梯度下降法
- 迭代逼近
- 两个问题
- 修改量的大小(learning_rate)
- 修改的方向
- $\theta_{i+1} = \theta_{i}-\eta\frac{df}{d\theta}$
- 步长,解决振荡问题
- 三种方案
- 批量梯度下降法
- 拿全部的样本训练,计算量大
- 随机梯度下降法
- 每次处理一个样本,更新比较快,但可能存在有标注错的样本,对训练操作影响
- 梯度是由一个样本计算得到的,并不能代表所有样本的梯度方向
- 小批量梯度下降法
- 折中的方案
- 批量梯度下降法
反向传播算法(BP:Back Propagation)
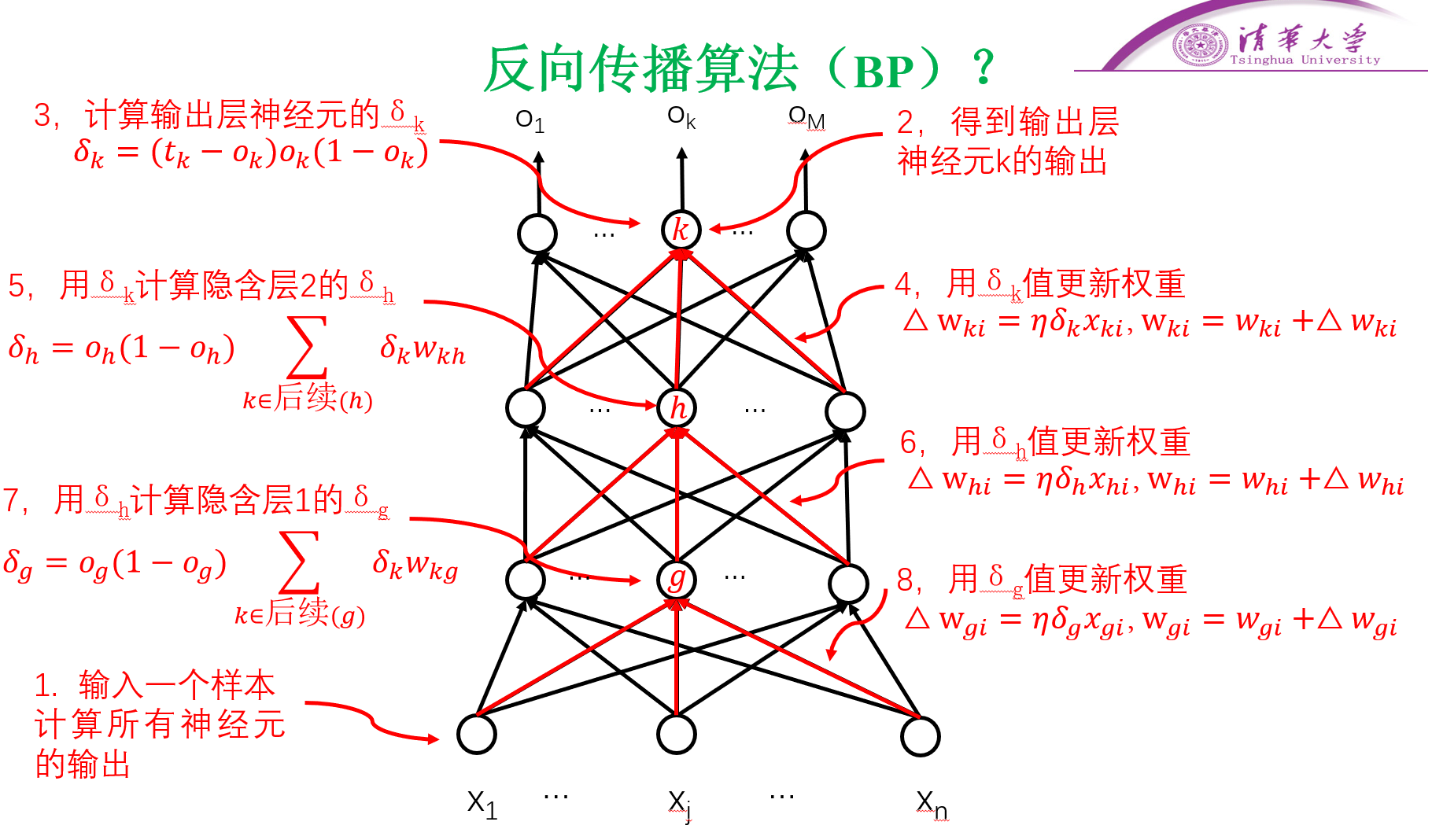
- 又称误差反向传播算法(最小化误差)
- 给出一种计算偏导的方法
- BP算法会因具体条件不同,算法会有差异,总体思想一样
- 上述BP算法的条件:
- 全连接网络
- 随机梯度下降法
- 激活函数:sigmoid
- 损失函数;误差平方和
- 上述BP算法的条件:
交叉熵损失函数
- 概率之和为1;概率在0~1之间
四、卷积神经网络§
全连接神经网络的缺点§
- 连接权值过多
- 计算量巨大,影响训练速度
- 影响使用速度
全连接神经网络与卷积神经网络的比较§
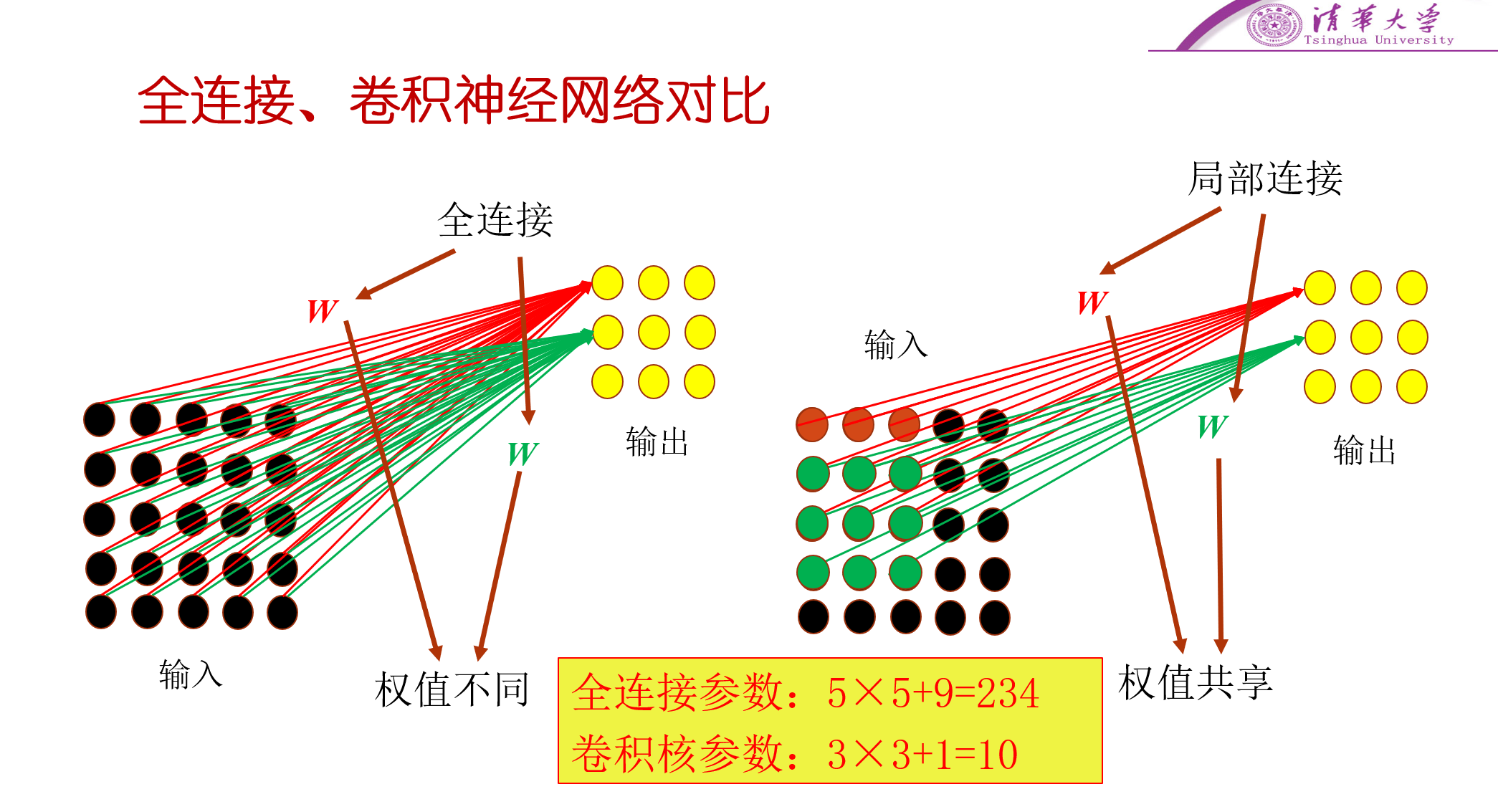
从看到的特征数量上比较,可以看到,全连接神经网络中,每个输出神经元都能够看到所有的输入神经元,也就是说能够看到所有的特征。而对于卷积神经网络,则采用的是局部连接,只能看到部分的输入,也就是只能看到局部的特征。
从权值的使用上来比较,在全连接神经网络中,每个输出的神经元与所有的输入神经元相连接,也就可以知道每个输出神经元用的都是不同的权值,而对于卷积神经网络而言,所有的输出神经元用的权值都是一样的,不同的地方只在于选取的输入特征不同,因此,通过这种方式大大减小了参数,也就意味着减小了计算量。
重要概念§
卷积核大小§
- 通常选取奇数作为卷积核大小,如3X3,5X5,7X7这样
填充§
- 当既不想改变卷积核大小,又想要让输入的大小与输出的大小相同的时候,可以给输入进行填充,如原本一个5X5的输入,通过外侧填充一层0,变为7X7的输入,则再通过3X3的卷积核,则可以得到一个和输入大小相同的,5X5的输出。
步长§
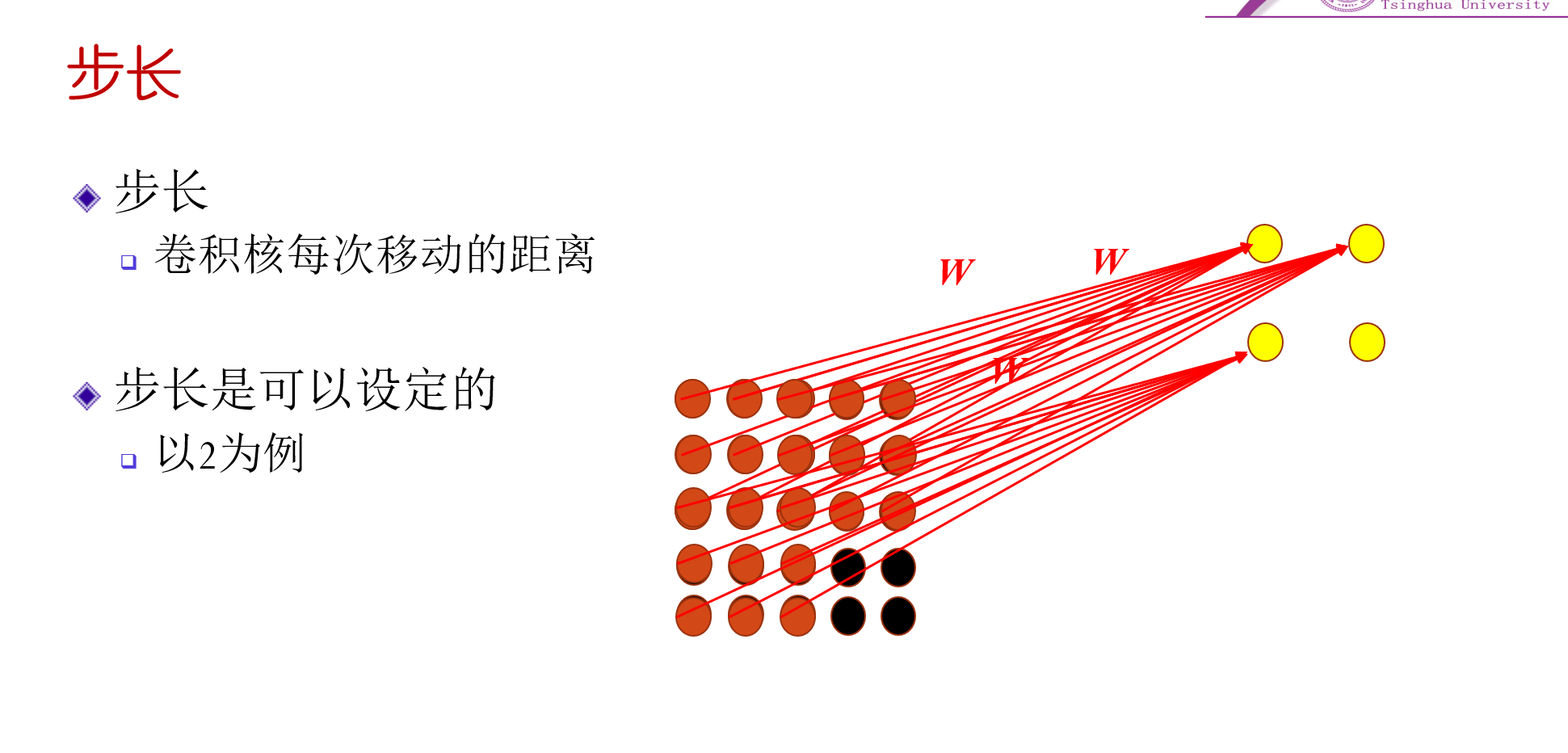
- 步长指的是卷积核每次移动的长度,步长为1,则卷积核在输入上每次只移动一行或一列,步长为2,则移动两行或两列,其他也都类似。
多卷积核§
- 多个卷积核
- 不同通道
多通道输入时的卷积§
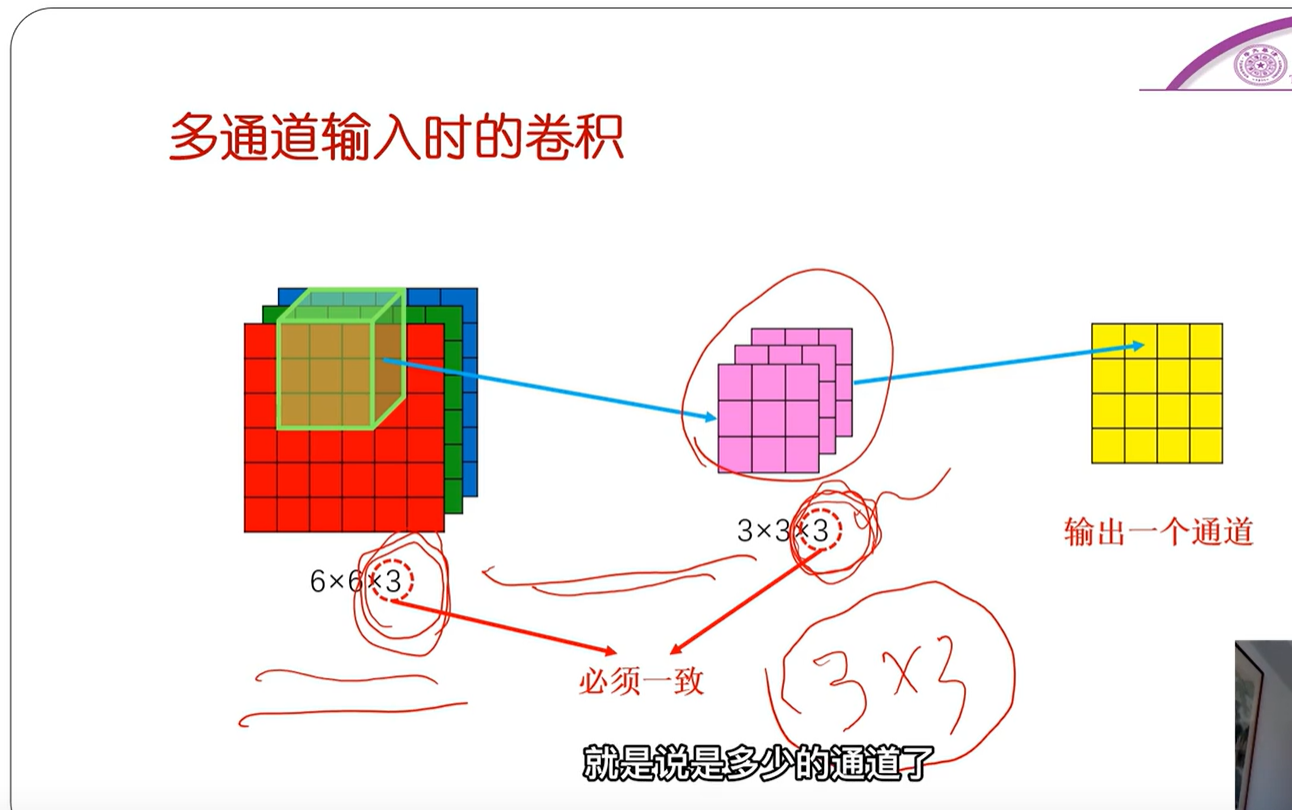
- 并不是说每个通道都单独进行卷积
- 而是把卷积核看成一个立体,就比如原本是二维的平面,现在无论是卷积核还是输入都是三维的立体了,如6X6X3,说明有3个6X6的输入,3通道。
- 运算上和二维一样,同样是对应位相乘求加权和。
- 输出的通道数只与卷积核的通道数有关,与输入的通道数无关。
卷积核的大小§
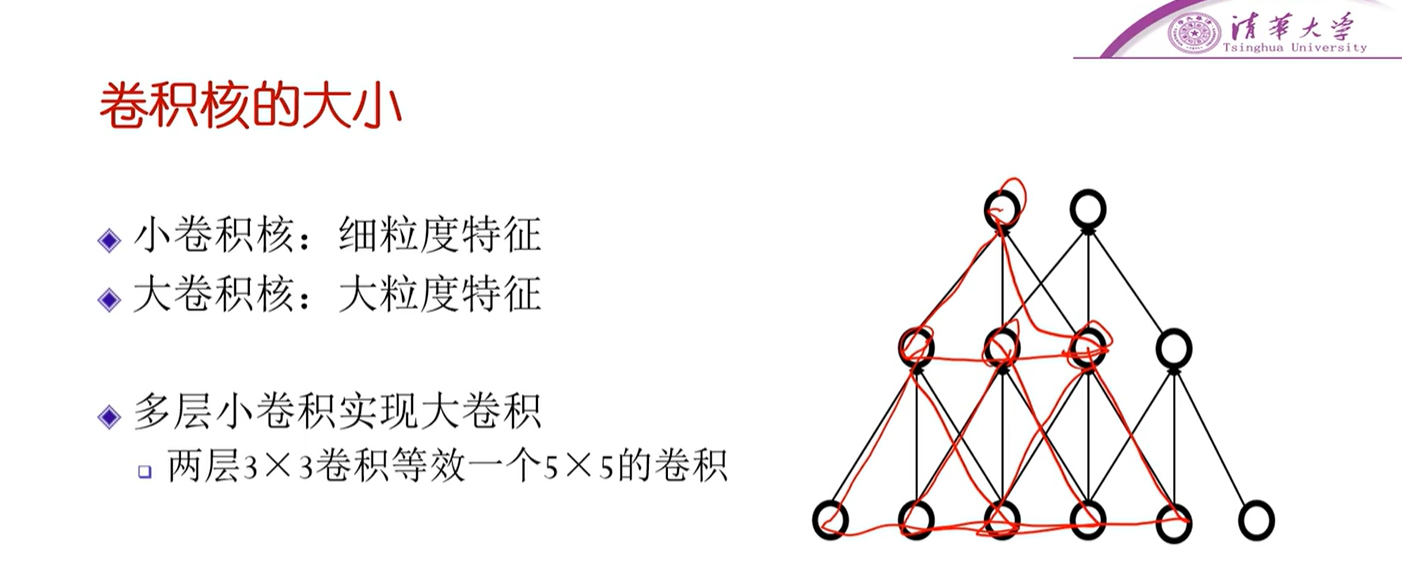
- 小卷积核:细粒度特征
- 大卷积核:大粒度特征
- 多层小卷积可以实现大卷积
- 可以看到最上面的神经元,虽然直接连接是三个神经元,但再往前看,可以发现最上面的神经元其实间接地连接着最小面的五个神经元。即图中的这个,两层的3X3卷积等效于一个5X5的卷积。
池化§
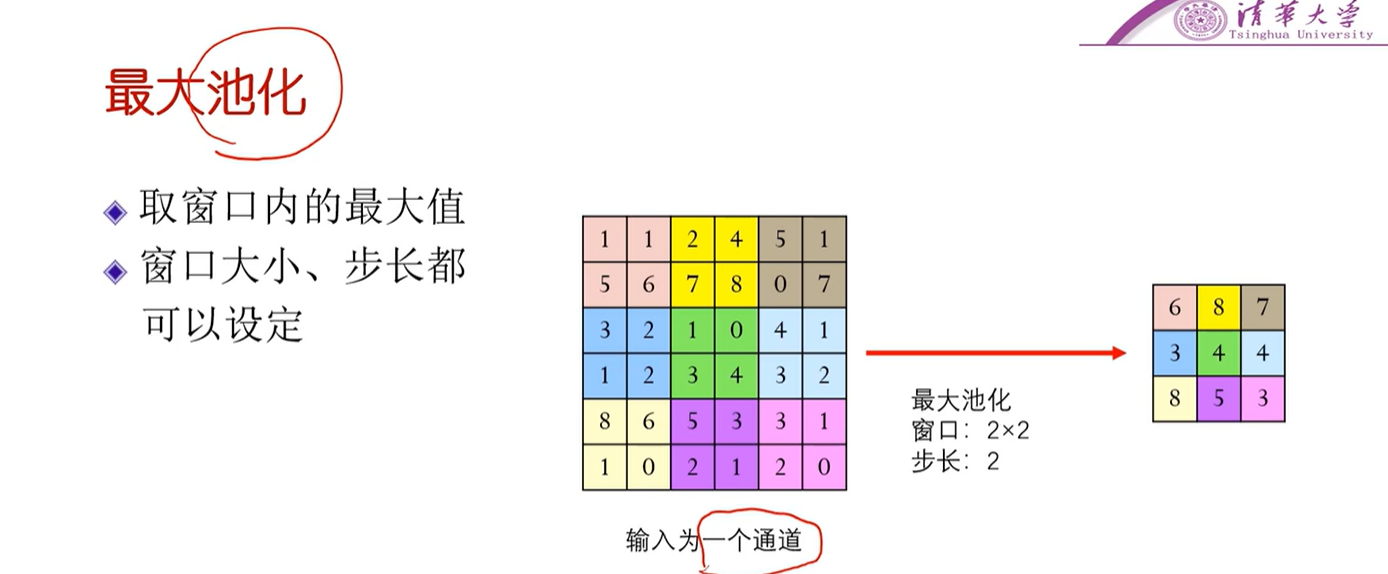
- 一种降维的手段
- 因为池化只是降维,要保留特征。因此,输入是多少个通道,输出就是多少个通道,不同通道的特征是不同的。
- 不仅可以取窗口内的最大值,也可以取窗口内的平均值(平均池化)
LeNet§
严乐春 提出的最初采用的卷积层的神经网络 图灵奖得主
VGG-16§
- 16层(一般把有参数(权值)的称为一层,如卷积层、全连接层,而池化层这些就不算了)
五、神经网络是如何实现的§
梯度消失问题§
- 出现原因
- 如Sigmoid,导函数为
- 解决方法
- 取ReLu整流函数,因为导数为1
- GoogLeNet
GoogLeNet§
- 高楼供水式 - 解决梯度消失的问题
- Inception(名称来源:盗梦空间-We need to go deeper!)
- 降维的Inception
文本的表示方式§
词向量§
one-hot编码§
- 稀疏矩阵
- 优点
- 编码简单
- 缺点
- 由于维度为词表大小,导致词向量维度过高
- 无法衡量每个词之间的相似性
分布式表示§
稠密矩阵
从不同角度上来对词进行表示
词嵌入
- 把词向量从高维空间嵌入到低维空间中的一个方法
- 即想办法从稀疏矩阵转换为稠密矩阵
语言模型§
- 用来计算一个句子的概率的模型
- n元语言模型
- 词袋语言模型
- 哈夫曼树
评论