在这一章中，首先大概讲了一些机器学习中常见问题的通用解决方法，告诉了我们可以怎样去处理。接着针对类神经网络训练不起来的问题，从局部最小值、批次与动量、学习率和损失函数四个点上分别进行了讲解。

一、机器学习任务攻略§

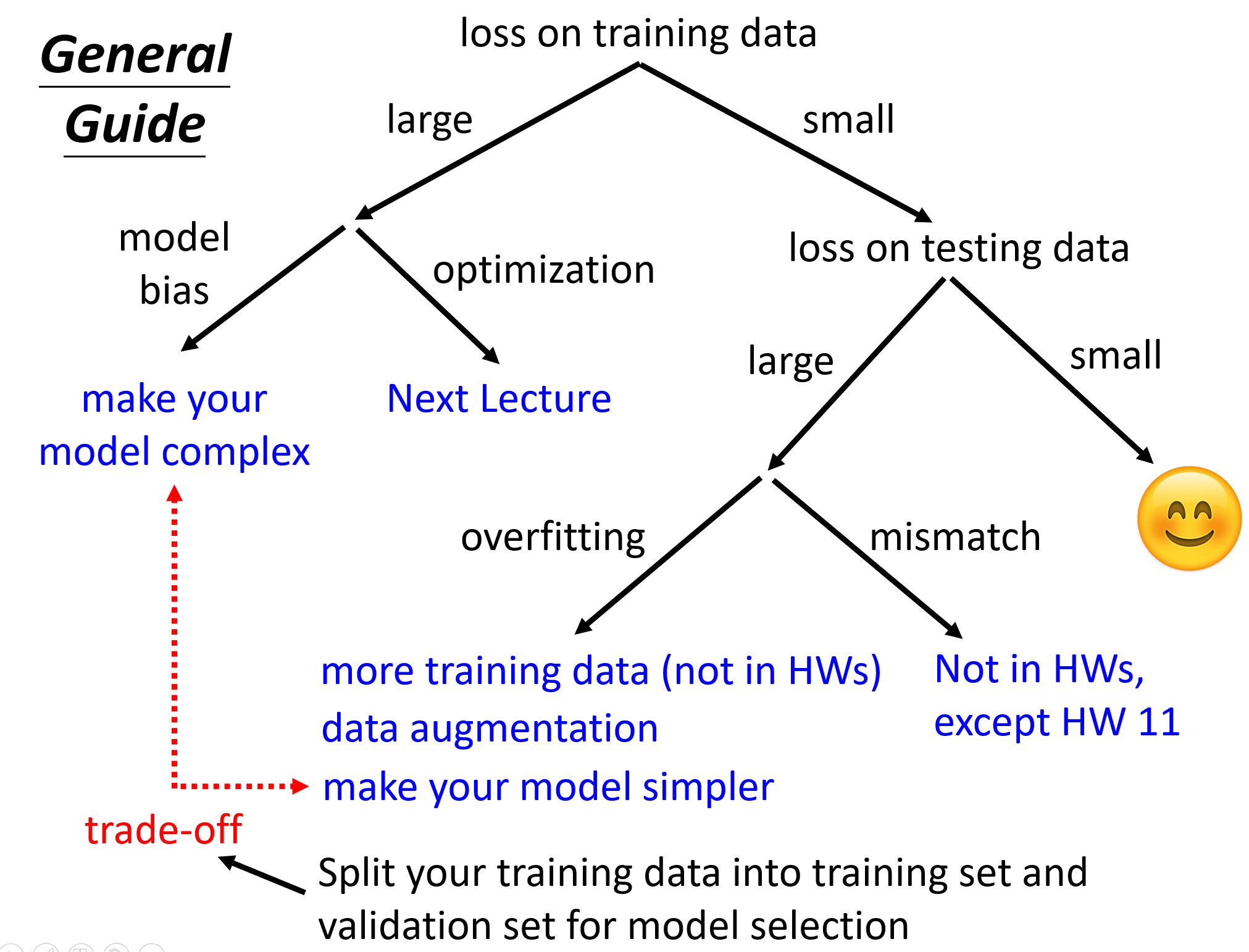
训练集上的loss太大了§

模型偏差大(Model bias)§

  • 模型太简单了（need more flexible）
    • 输入更多的特征$x_i$
    • 使用更多的神经元(neuron)
    • 增加网络的深度(layer)
  • 当然也是不能让模型过于的复杂，选择一个恰当的点，这是一直需要考虑的问题
    • image-20221127171221552

优化问题§

Model Bias or Optimization Issue ?§

  • 通过比较不同复杂度的模型的loss
    • 在简单的模型能够得到比较低的loss，但是却在复杂的模型上得到的loss更高，那这个时候就可以考虑是Optimization的问题，因为之前有说，增强模型复杂度，可以缓解Model Bias，但现在明明模型更复杂了，但是loss反而增大了。
  • 因此在处理一个新问题时，可以先选择一个简单的模型，线性模型，或者传统机器学习处理，这样一般存在优化的问题。

训练集上的loss较小，测试集上的loss大§

Overfitting§

  • 更多的训练数据（more training data）
    • 视频中有说更多的数据能够更好地限制住模型s
    • 但更准确地说应该是更多的训练数据，会符合整体数据的分布，也就是说只要我的训练数据的分布得到的模型，能够和测试数据的一样，那就能够得到比较好的结果。
  • 数据增强（data augmentation）
    • 像图像，可以通过平移、翻转等操作增加出更多有意义的数据
    • 信号的话，也可以通过偏移，来增强数据
  • 限制模型的复杂度
    • 简单一些的模型对应的解也会更少，所以可以更快找到比较优的结果（当然也是不能让模型过于简单，太简单的话又会回到欠拟合的情况下）
    • Less parameters(减少神经元)，sharing parameters(CNN)
      • image-20221127171029692
    • 更少的特征
    • 早停（early stopping）
    • 正则化（regularization）
    • Dropout

mismatch§

  • 有点类似overfitting，但overfittin更多说的是训练和测试数据的分布应该是差不多的
  • 但是在mismatch的情况下，由于测试数据的分布和训练数据的分布差距很大，这样在测试集上的结果肯定是不准的。

将训练数据划分为训练集和验证集§

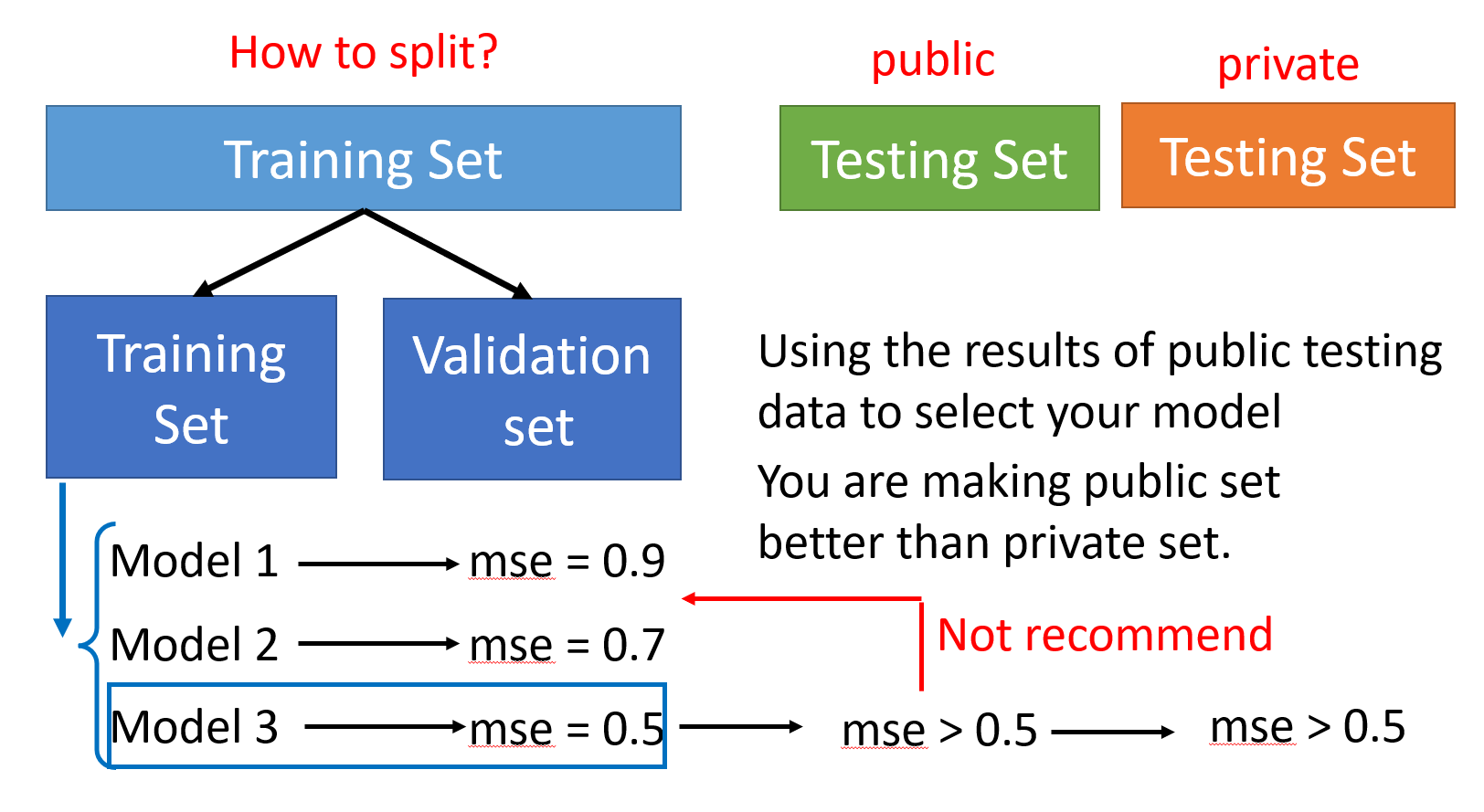
image-20221127182418546

这里考虑的点，让我有种醍醐灌顶的感觉。

就是为什么在比赛通常会划分为public和private的测试集？

  • 以前我个人以为只是做进一步的评估，这样会更充分一些，因为测试数据越多也越有说服力，或者说private的测试集的分布会有些差异。
  • 但其实我们的前提就是训练集和测试集的分布要相似的，这是需要明确的。
  • 而为什么会有private测试集，是因为我们在public的测试集上能够看到得分，那只要不断地对照在public上的分数，随机生成结果提交，最终一定能得到比较高的分数，但这其实是毫无意义的。
  • 所以需要将训练数据拆分出验证集，然后我们根据验证集上的最好结果，来进行提交。这个时候，虽然能够看得到在public测试集上的得分，但最好也不要去在意，因为如果这个时候又去根据public上的结果去调整，那又回到了上个小点追求高的public测试集的分，但在private上得分低的情况。
  • 因此，只要关注验证集就好，那为了让验证集上的结果也更可靠，可以使用K交叉验证(K-Fold cross validation)的方法。

二、类神经网络训练不起来怎么办？§

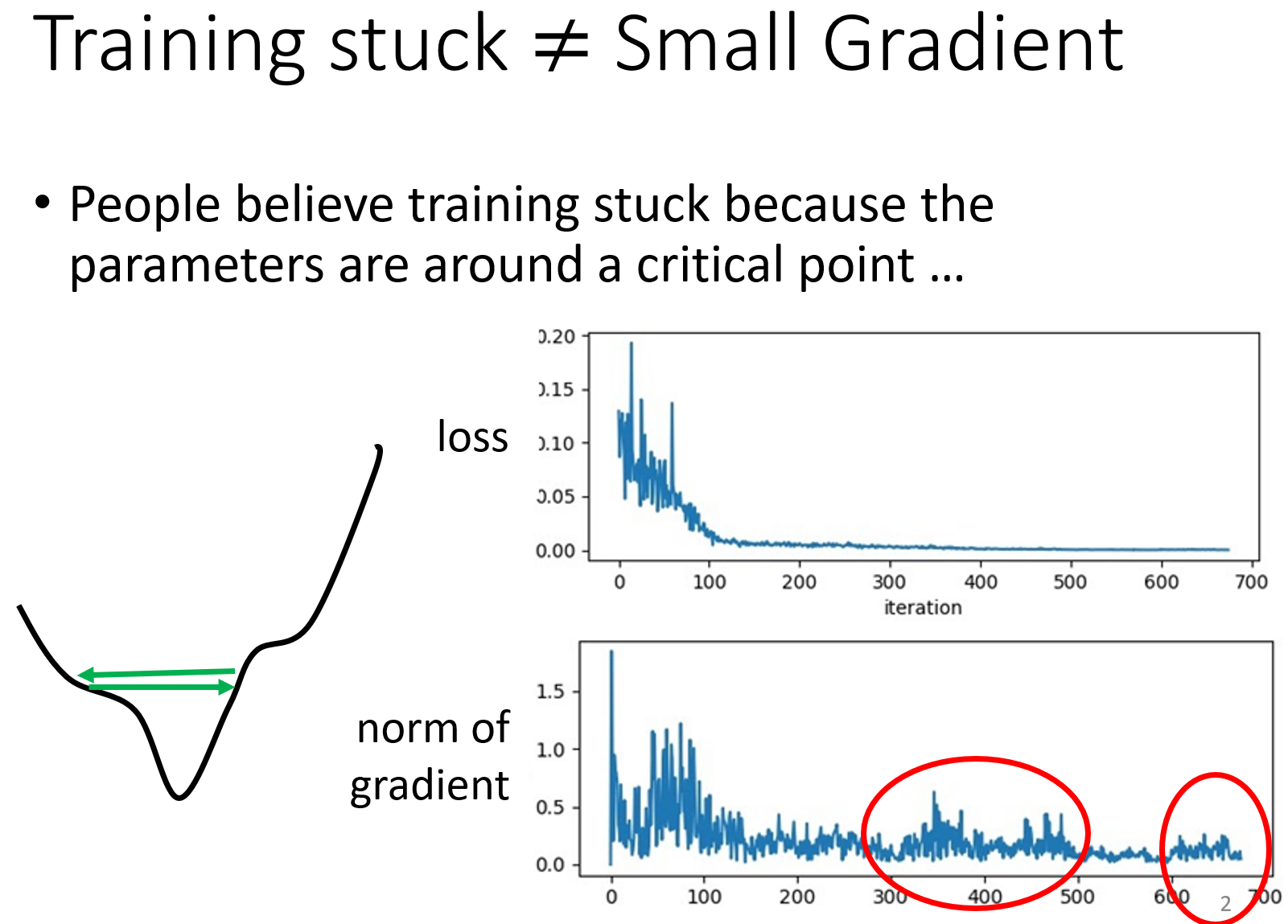
李宏毅老师说的还挺有意思的，一开始说SGD真正的痛点不是局部最小值，可能是遇到了鞍点，之后又说，可能loss不动的时候，你的gradient仍然还很大，不是0，也就是你根本就没有遇到critical point（local minima和saddle point）的问题，会是learning rate太大会发生振荡。

1. 梯度为0，导致网络不再更新§

  • Local minima VS. Saddle point
    • 首先需要明确，在SGD优化下，并不只有局部最小值的问题，还有鞍点（Saddle point）的问题
    • 在局部最小值的时候，已经是这个区间内的最小值了，但在鞍点时，虽然一阶导为0，但是鞍点在这个区间内，既不是最小值，也不是最大值。

数学解释§

image-20221127211433066

从上图可以知道，我们将损失函数$L(\theta)$近似为了一个多项式，其实也就是高数里的泰勒展开，这里放一下在某一点的泰勒展开的定义：

若一个函数在某个区间内可以求任意阶的导数（例如幂函数，三角函数，指数函数，对数函数等），那么这个函数可以用一个多项式近似。

对应于我们这里就是$\theta^{’}$是一个特定的点，而$\theta$是$\theta^{’}$附近的点（左右），这里的$g$就是一阶导，$H$就是二阶导（由于是多元微分中，所以是一个海森矩阵）。从这里就已经可以理解，为什么我们每次在讲loss的时候，总是会说到一阶动量和二阶动量，因为他们与loss的优化是密切相关的。

image-20221127212308723

那当我们的梯度为0，陷入到了局部最小值或鞍点的时候，那$g$为0，按上图就直接去掉了，这时就只需要考虑后面的一部分。看完下面的解释，就终于可以理解以前为什么老是说一个函数的海森矩阵半正定就是一个凸函数了。

image-20221127212836387

可以看到，如果$H>0$，也就是$H$正定，那可以得到极小值，这和以前高数中学的一样（一阶导为0，二阶导大于0）。类似的，$H<0$，$H$是负正定，得到极大值（不过这里不用太关注极大值的问题，因为如果目标是最大值，那就加个负号，或倒一下，就变成求最小值了）。最后的一种情况，也就是以前最迷惑的一点，$H$既可以大于0，又可以小于0，则可以得到这个点是鞍点，在鞍点的时候，我们是还可以继续走，找到更小的loss的。

对于半正定其实也是类似的，就假设最极端地情况，$H$为0了，那这样的结果也就是周围的点和$\theta^{’}$相等了。

海森矩阵解决鞍点问题§

当遇到鞍点问题的时候，此时是可以根据海森矩阵的特征值来求解参数的优化方向的：

  • 因为是鞍点，所以是存在小于0的特征值，根据这个特征值求得对应的特征向量
  • 可得下一步移动的方向就是该特征向量的方向

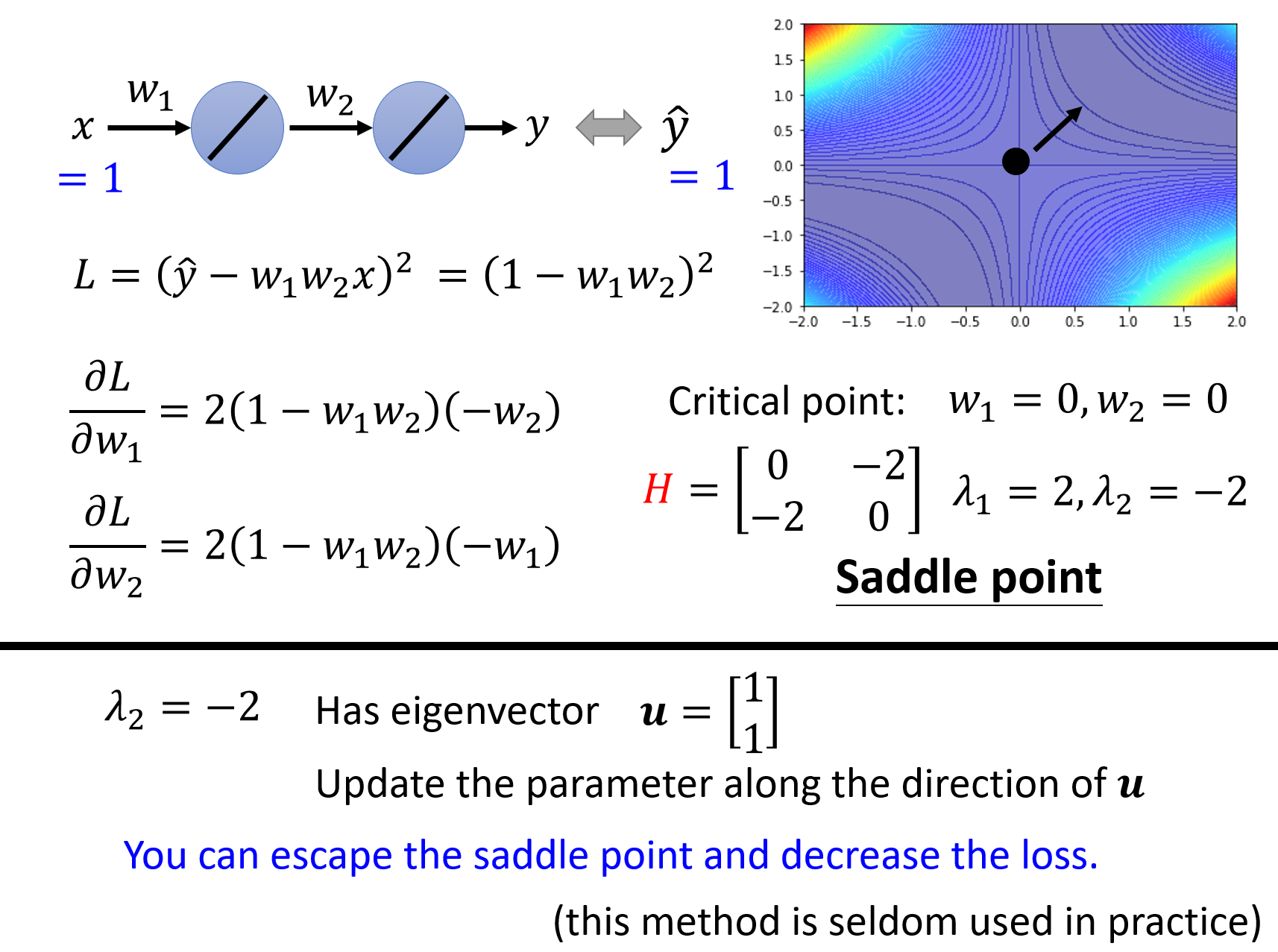
但是也有提及这个方法在实际中是很少用到的，计算量大。这个问题感觉可以类比为什么我们通常是用梯度下降的方法来优化，而不是直接去求一阶导数为0的（当然这只针对凸函数），但计算机是更适合去做重复性的事情。

在训练中，鞍点or局部最小值，哪种情况比较多？§

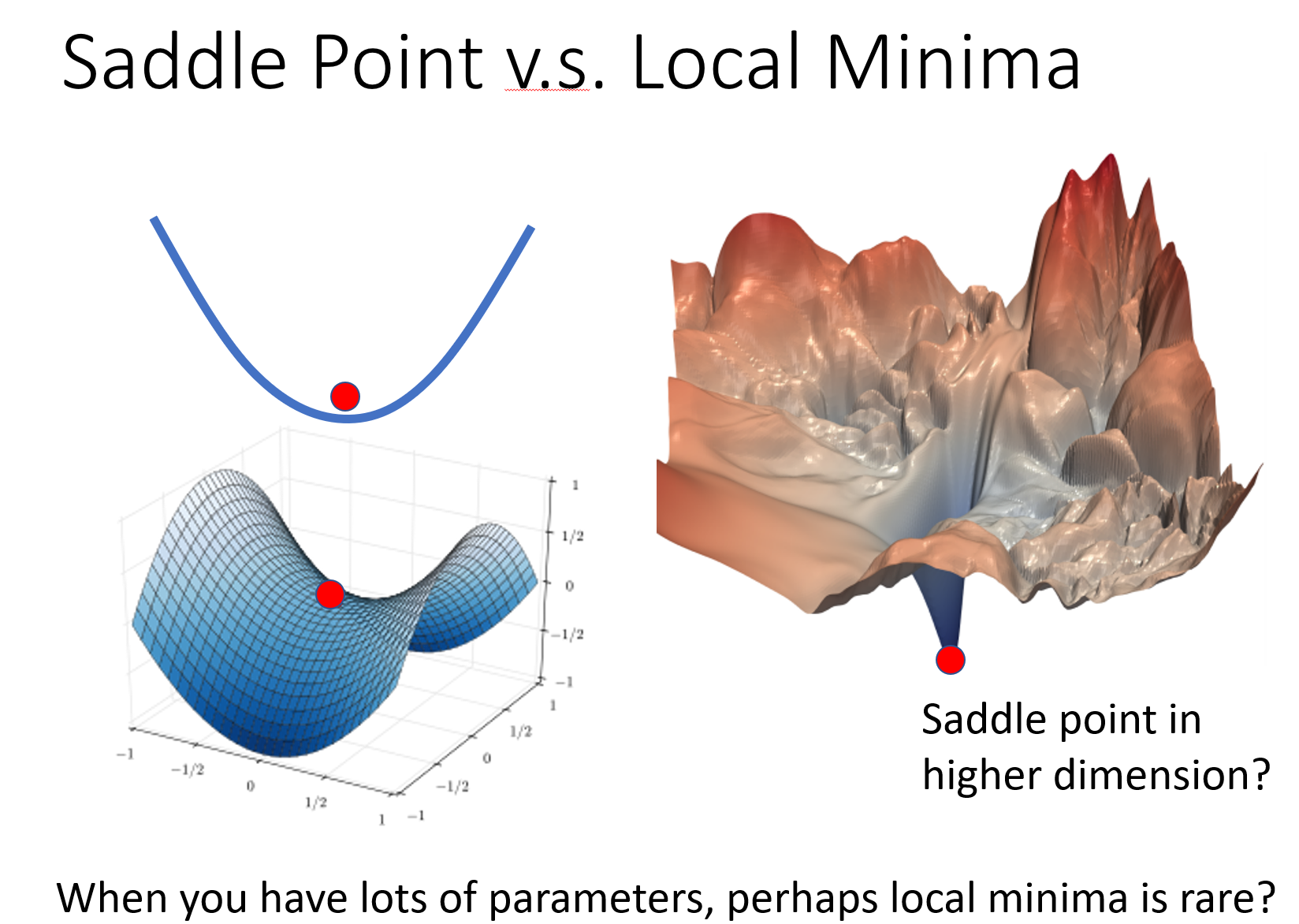
image-20221128123423468

结论是鞍点的情况是远多于局部最小值的情况的，即使是遇到了局部最小值的情况，在更高的维度下也是会转变为鞍点问题。

2. Batch & Momentum§

Small Batch or Large Batch?§

  • 大Batch的速度其实比小Batch要快（因为有GPU并行运算）
    • 跑一个大Batch和小Batch的时间差不多，但是小Batch需要循环迭代更多次数
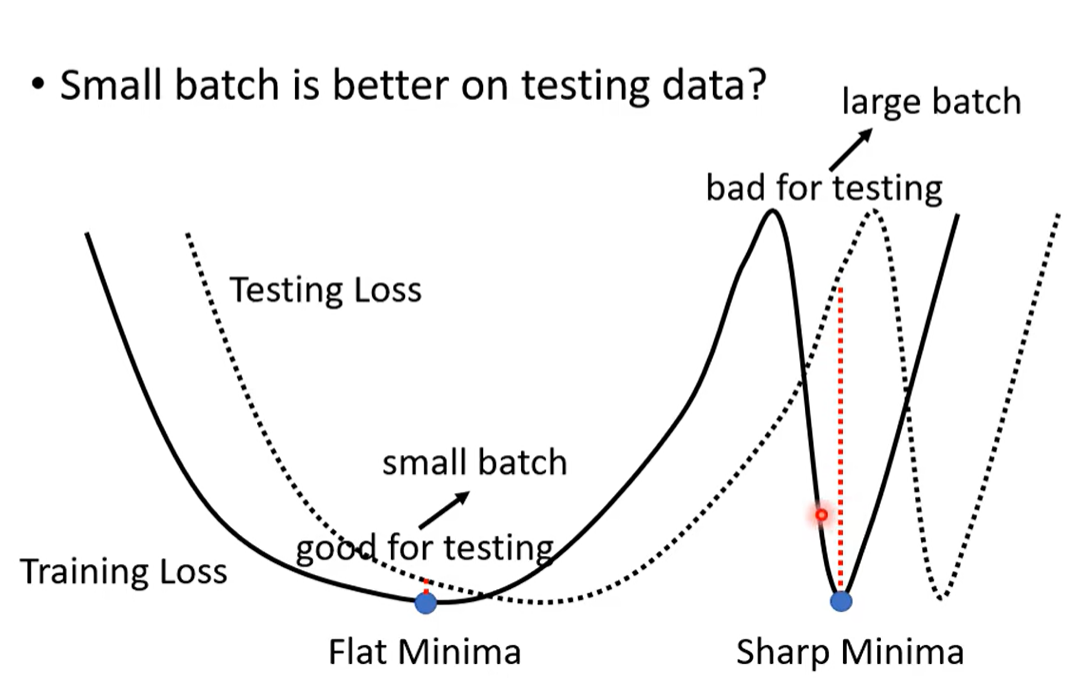
  • 小Batch的效果往往会比大Batch的效果要好
    • 给出的解释是小的Batch更加Noisy，每一次会得到的loss差异大，而大Batch下求的平均loss会平滑掉，没那么容易冲出局部最小值。
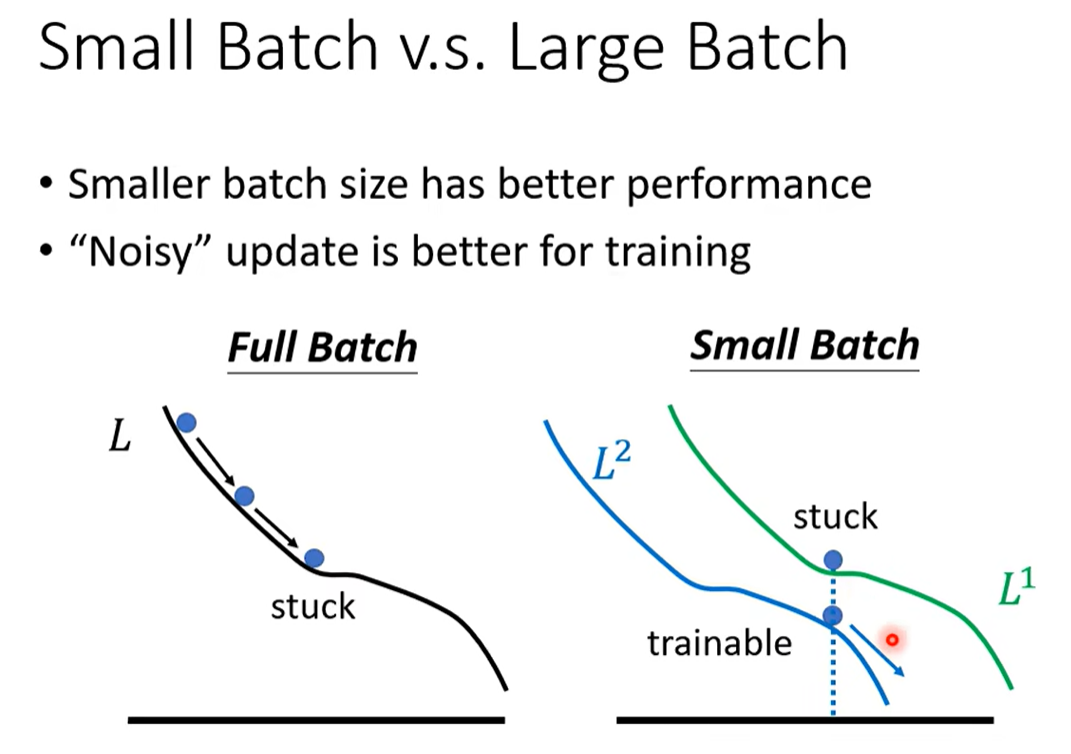
    • image-20221128125720020
  • 小Batch的泛化能力会更好（大小Batch在训练集上达到相同的准确率，但是小batch在测试集上的表现更好）
    • 小的batch更容易冲出狭窄的loss最小值，停留在比较宽广的最小值
    • 测试集和训练集的分布会有些差异，若停留在训练集狭窄的最低点，但在测试集上的差异可能就会比较大
    • image-20221128130159679

Momentum§

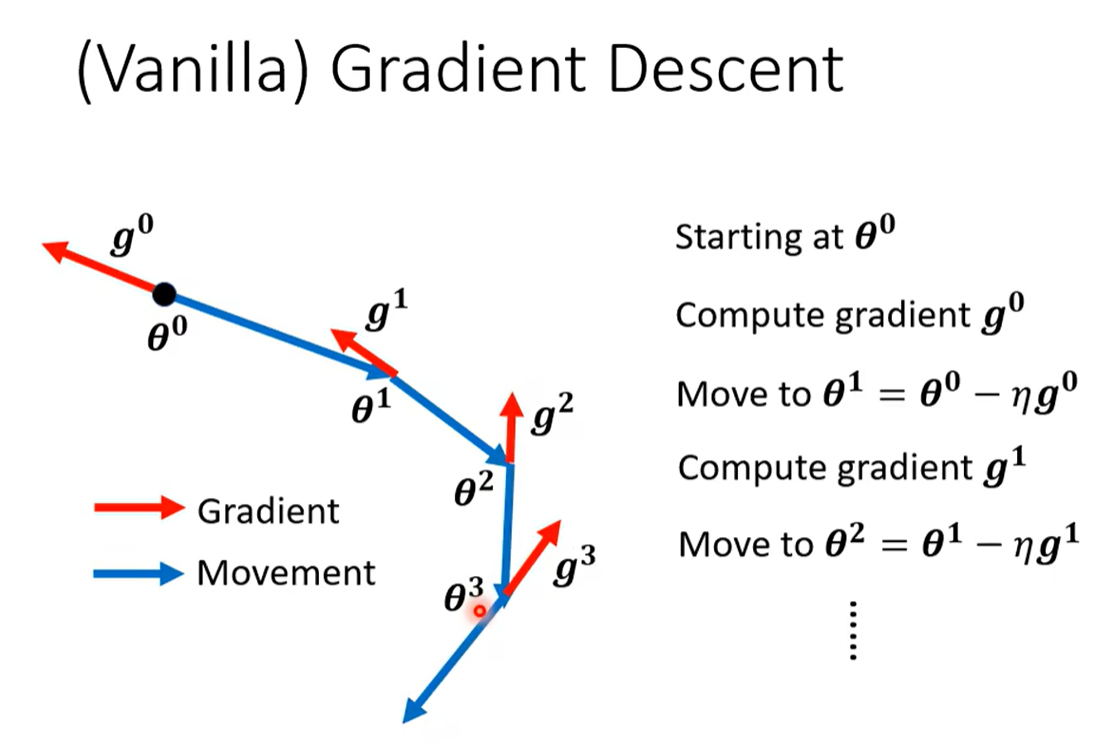
在提及Momentum之前，可以先看一下常规的梯度下降法：

image-20221128191552643

{{ }}这里的梯度下降叫作Vanilla的梯度下降，Vanilla是香草的意思，还挺有趣的。{{ }}

在该优化下，可以知道每次更新的方向是本次梯度的反方向，也就是说只和本次的梯度有关，和之前的都无关。这样导致的结果就会有，如果目前所在点的梯度为0了，那参数就不会再更新下去了；如果目前梯度很小，那就会走的很慢。

所以引出了Momentum：

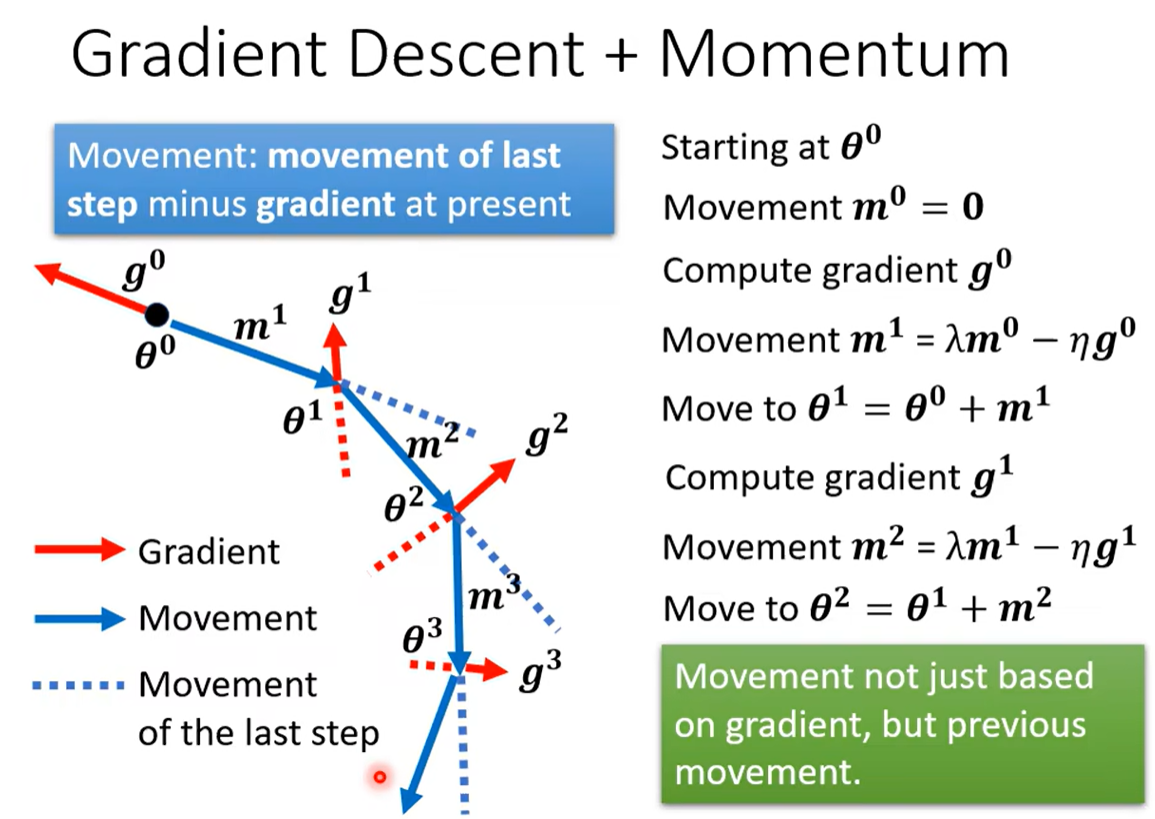
image-20221128192558377

这里关于Momentum的梯度下降可以有两个解释：

  • 可以把新的更新方向看作是当前梯度的反方向和之前的方向之和的方向，也就是既受到之前方向的影响，又受到本次梯度方向的影响，类似于惯性的感觉。
  • 或者也可以看作当前更新的方向是之前所有梯度的累加和的方向，例如对于$m^2$，可以是$m^2 = \lambda m^{1} - \eta g^{1} = \lambda (\lambda m^{0} - \eta g^{0}) - \eta g^{1} $，可以看到和每一个$g^{i}$有关。

3. Adaptive Learning Rate§

这一小节有给我纠正一个错误的观点，就是之前一直任务自适应学习率的优化方法中说的这个自适应，只是说学习率会随着迭代次数的变化而发生变化，但除了这一点，其实这里的自适应还是指会根据不同的参数来选择学习率的大小，这一点很重要。因为假设有两个参数，一个参数目前的梯度变化很小，而另一个参数的梯度变化很大，然后我现在的学习率如果很大的话，虽然对于那个梯度小的参数来说可能会走的更快些，但这会导致那个梯度大的参数的变化会更大，双倍增大，这也就是为什么会出现振荡，loss不变了，梯度却不为0的情况。

在这一小节中就有说到当loss不再发生变化的时候，可能并不是因为梯度变为了0，而可能是因为学习率太大了，发生了振荡。如下图所示，卡在了上面，却下不去。

image-20221129190502806

所以，就会选择说，去减小它的学习率：

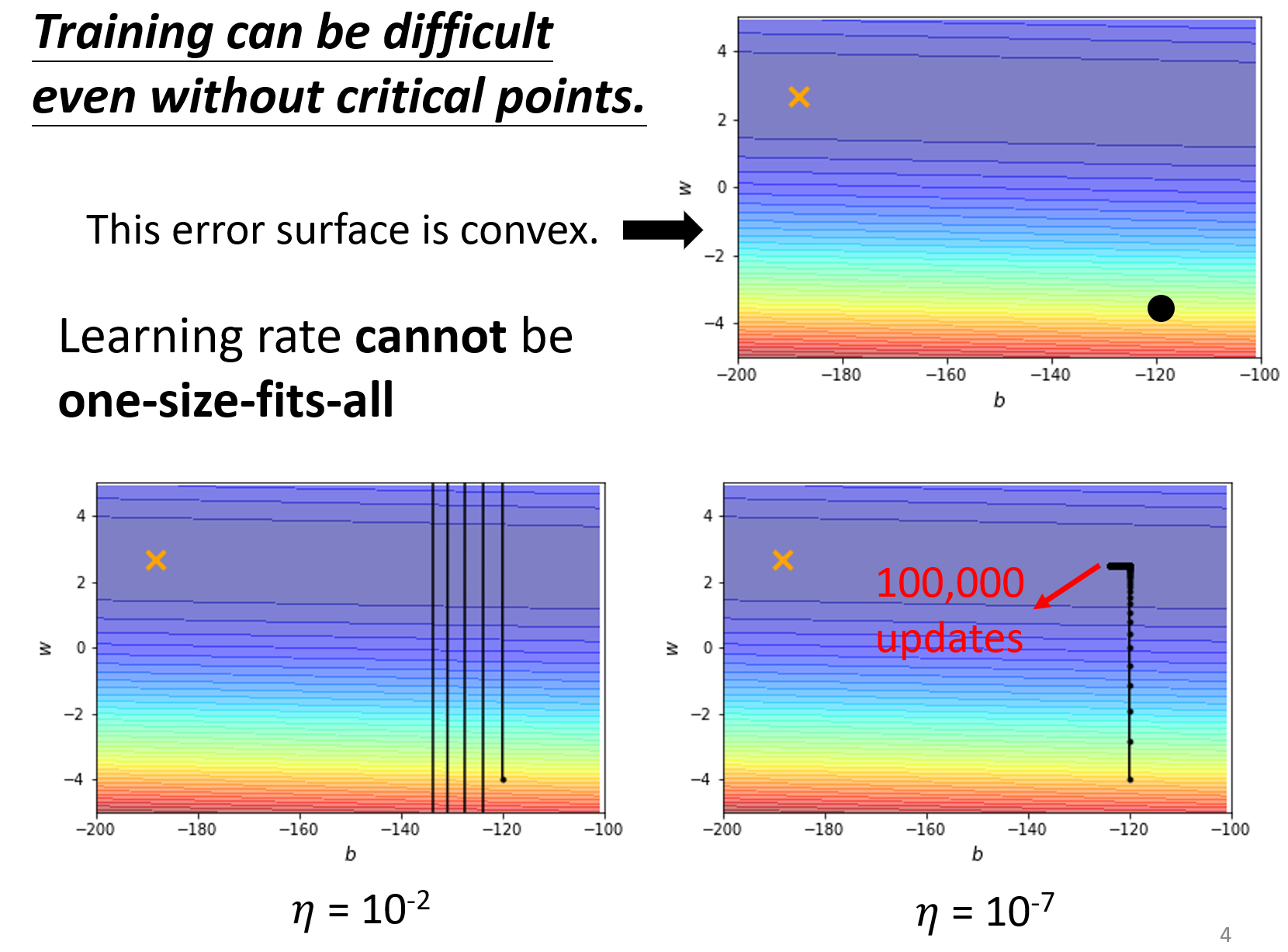
image-20221129192236969

但是会发现，在减小了学习率后，确实往loss小的地方走了，但是只有纵向走的很好，横向却很难走的动。这是为什么？我们可以看到$w$和$b$使用统一的学习率下，因为纵向$w$的梯度比较大，所以在学习率减小后，不发生振荡了，开始走下loss低点，但是对于横向的$b$来说，它本来所在的地方就已经很平坦了，梯度很小了，再去减小它的学习率的话，那它的更新步伐就更加的慢了，这也就是为什么横向会走不动的原因。

优化器§

为了解决上面的问题，也就会有各种新的优化法。

这里李宏毅老师其实会说的比较简单，讲了Adagrad，RMSprop和Adam，对于更详细的关于各种优化器的解释，推荐看这篇知乎的文章：一个框架看懂优化算法之异同 SGD/AdaGrad/Adam - 知乎 (zhihu.com)。

Adagrad§
  • 引入了梯度的平方和的根来控制学习率的变化，$w_{i}^{t+1} \leftarrow w_{i}^{t} - \frac{\eta}{\sigma_{i}^{t}}g_{i}^{t}$，其中的$w_{i}^{t}$指的是第$i$个参数，$t$指的是第$t$次迭代更新，$g_{i}^{t}$也就是当前参数在本次迭代的梯度了，而$\sigma_{i}^{t} = \frac{1}{t+1} \sum_{t=0}^{t} \sqrt{(g_{i}^{t})^{2}}$，会不断地累加之前的梯度。
  • 优点：可以根据历史梯度大小，控制更新步长，若梯度一直很小，那就会走的步长大些，梯度要是一直很大，那就会走慢一些。
  • 缺点：由于会累积之前所有的梯度，所以会随着迭代次数的增加，分母越来越大，到最后可能导致$\frac{\eta}{\sigma^{t}_{i}}$趋近于0，不再更新参数，但loss却并没有下降到足够低。
RMSprop§
  • RMSprop为了解决Adagrad的所有梯度一直累加的问题，将梯度累加的策略进行了更改。使用了到了指数移动平均的方式，$\sigma_{i}^{t} = \sqrt{\alpha \sigma_{i}^{t-1}+(1-\alpha)g_{i}^{t}}$，通过这种方式累加效果可以证明等价于只考虑最近$\frac{1}{1-\alpha}$迭代次数内的梯度，所以就是不考虑全部的，只考虑最近的，这样就不会一直累加导致很大了。
Adam§
  • Adam = RMSprop + Momentum
  • 和之前的Momentum累加的方式也有差异，这里的$m$也是使用了指数移动平均的方式累加的
  • image-20221129201004058

Learning Rate Schedule§

虽然对各个不同参数的更新进行了自适应，但是学习率如果保持不变的话，还会出现下面左图的开始振荡的情况，这里的原因是因为一直在一个比较平坦的地方，梯度一直很小，所以导致$\frac{\eta}{\sigma}$变的比较大，出现了振荡。

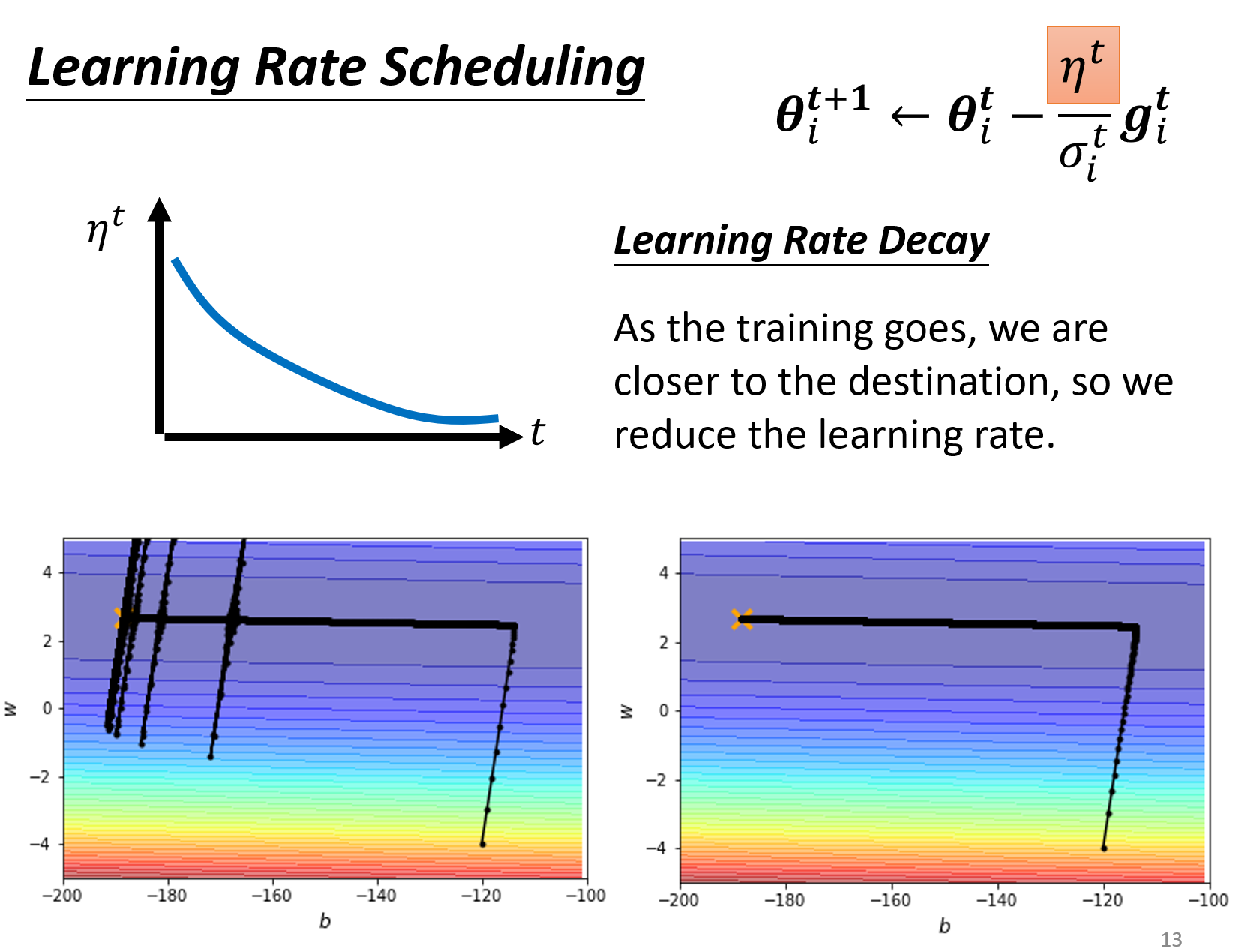
image-20221129201402018

所以，为了解决这个问题，又引入了学习率衰减的策略。同时，除了学习率衰减的策略外，还有一个warm up的策略，会先提高下学习率，之后再降低学习率，这个学习率调整的策略在residual network和transformer中都有用到，属于黑魔法的范畴。

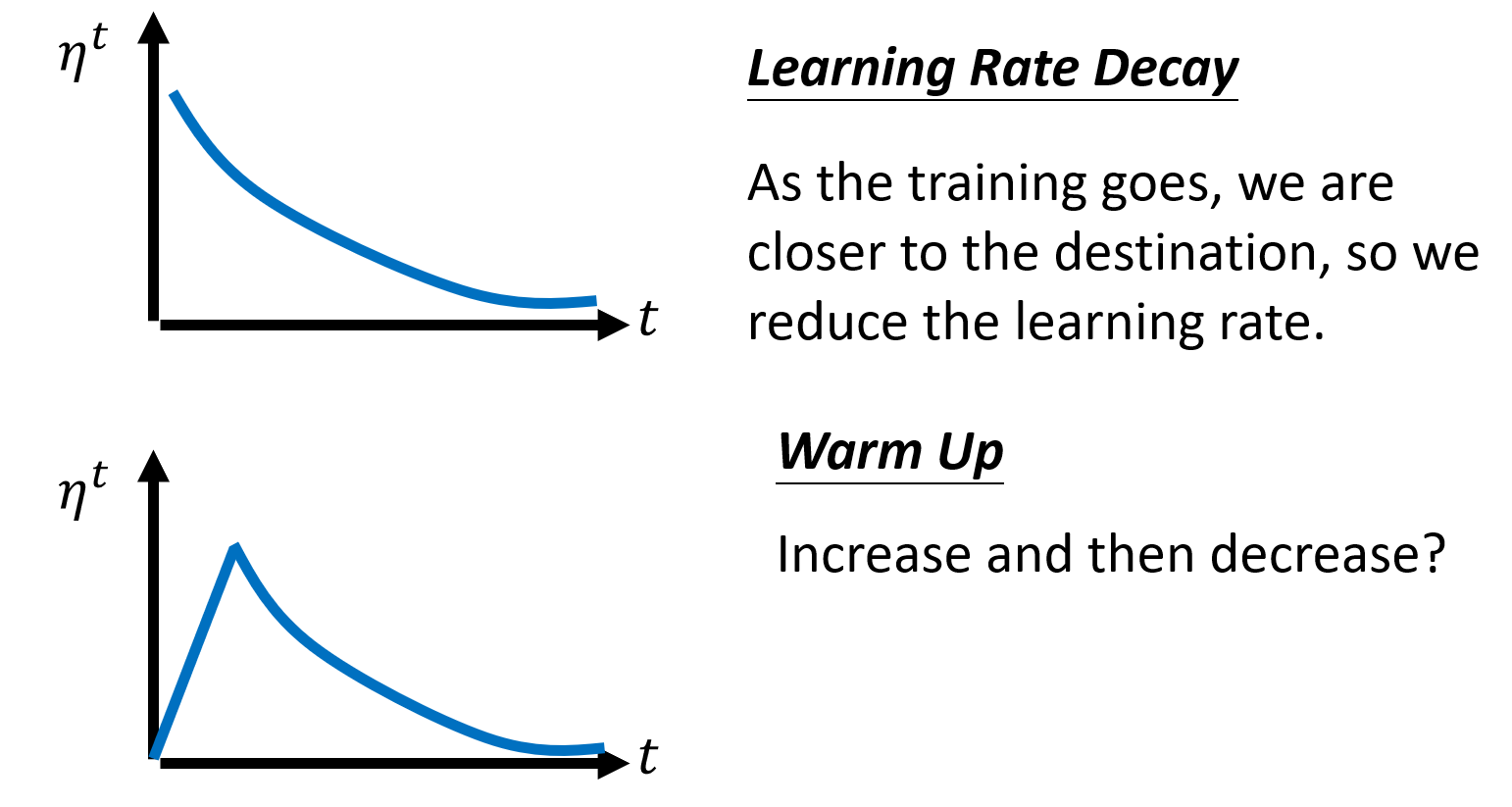
image-20221129201925580

下面是对本小节的内容的总结，从一般的优化方法，到各种不同的提升策略，主要做的事情也就是会针对不同的参数进行不同步长的更新。

image-20221129201322668

4. Loss function§

cross-entropy§

交叉熵损失函数，常用于分类问题中，其实就是负log的最大似然估计方法。在多分类下，通常是和Softmax激活函数同时使用的，这一点在pytorch中就是如此实现的。 $$ \ell(x, y) = L = {l_1,\dots,l_N}^\top, \quad l_n = - w_{y_n} \log \frac{\exp(x_{n,y_n})}{\sum_{c=1}^C \exp(x_{n,c})} \cdot \mathbb{1} $$ 这里一开始不是很懂为什么torch他这里用了$w_{y_n}$，还以为是训练中的参数$w$，想着怎么出现到这里来了。其实这里$y_n$应该指的是第$n$个输入对应的target，也就是类别，所以这里的$w$其实是给不同的类别赋予的权值，如果不特别设置权值，那自然就都是1的（会转换为one-hot编码），如果有对不同类别设置权值，那就是在原来1的情况下再乘以一个权值。

nn.CrossEntropyLoss()
"""
This criterion computes the cross entropy loss between input logits and target.
Note that this case is equivalent to the combination of :class:`~torch.nn.LogSoftmax` and
:class:`~torch.nn.NLLLoss`.
"""

这里说的logits，其实就是经过了Softmax后的值。而且后面也有说，这个函数是LogSoftmax和NLLLoss的组合，所以这也是为什么通常在用torch写神经网络完成多分类时，最后一层并没有加Softmax函数的原因，毕竟torch在交叉熵损失函数中已经有这个处理了。关于NLLLoss的全称也就是之前说过的：

使用Softmax的两点作用：

  • 把数据统一到0~1之间，且之和为1，类似于概率的形式
  • 加大不同数值之间的差异性，因为输入在softmax的作用下，都会变为以$e$为底的指数函数的幂数，自然就加大了数值之间的差异。
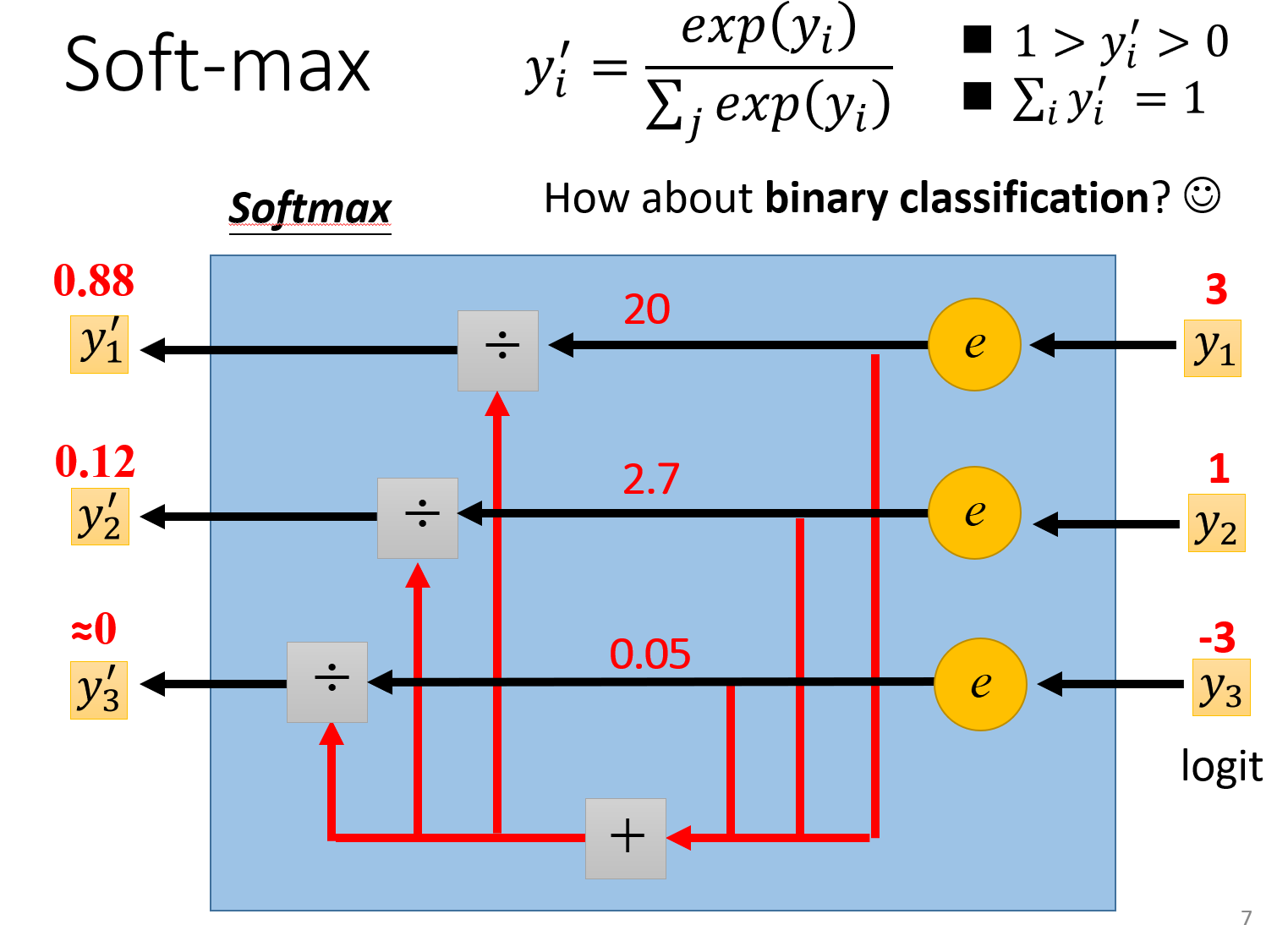
image-20221203095516197

这里的图就有直观的反应了softmax上面说的两个作用，范围为0到1，输入3和1，转换为了20和2.7。

改变loss function可以改变优化的难度§

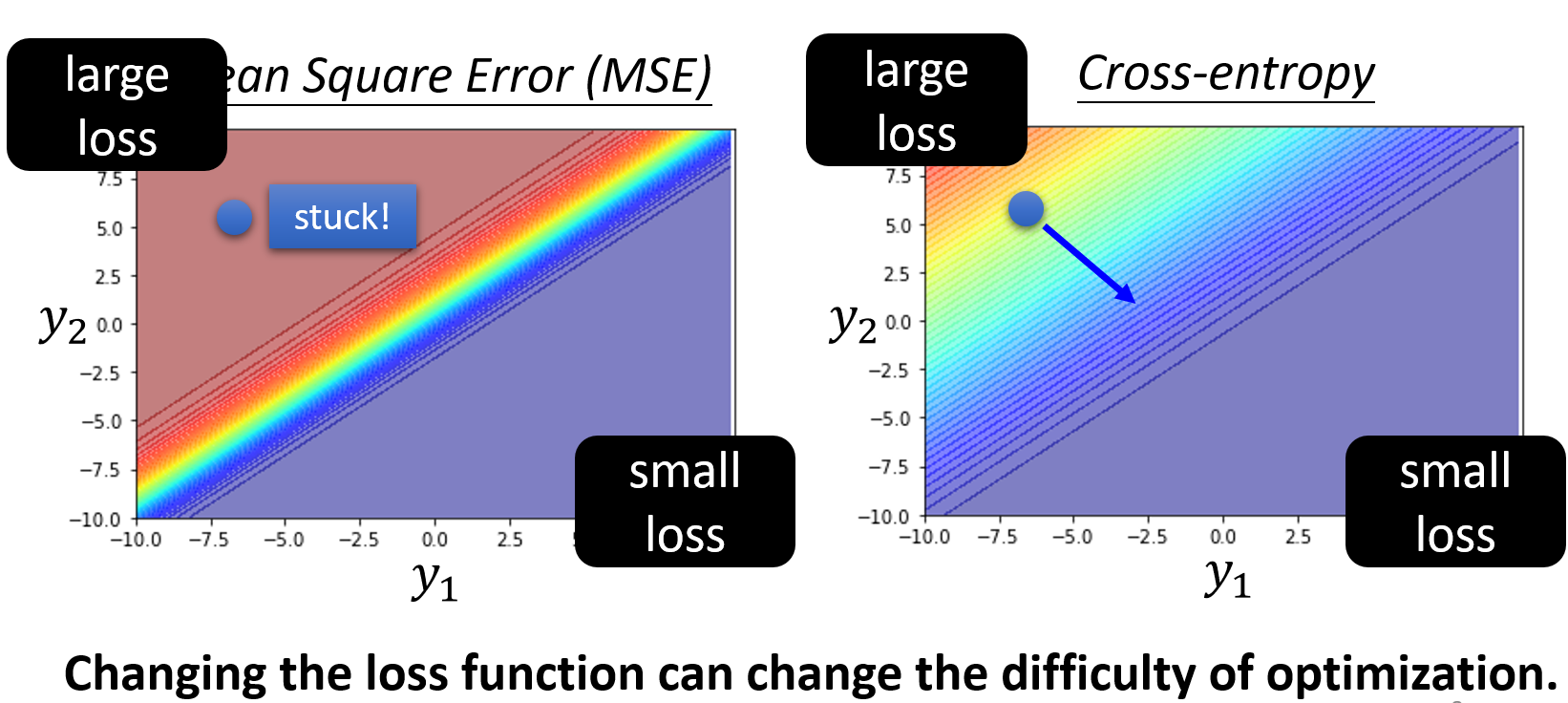
image-20221203102128612

这张图感觉就挺有意思的，在分类任务下，左边用的是MSE这个function，右边是cross-entropy，能够很明显的看到cross-entropy的梯度下降方向就很明显，loss从大到小。而MSE下，如果一开始初始化在左上角的话，高loss，而且梯度很小，就很难移动。

5. Batch Normalization§

之前有说一个合适的损失函数，是可以让崎岖的error surface能够变的平滑，更容易优化的。那么除了选择合适的loss function外，也还可以通过normalization的方式去加快训练。